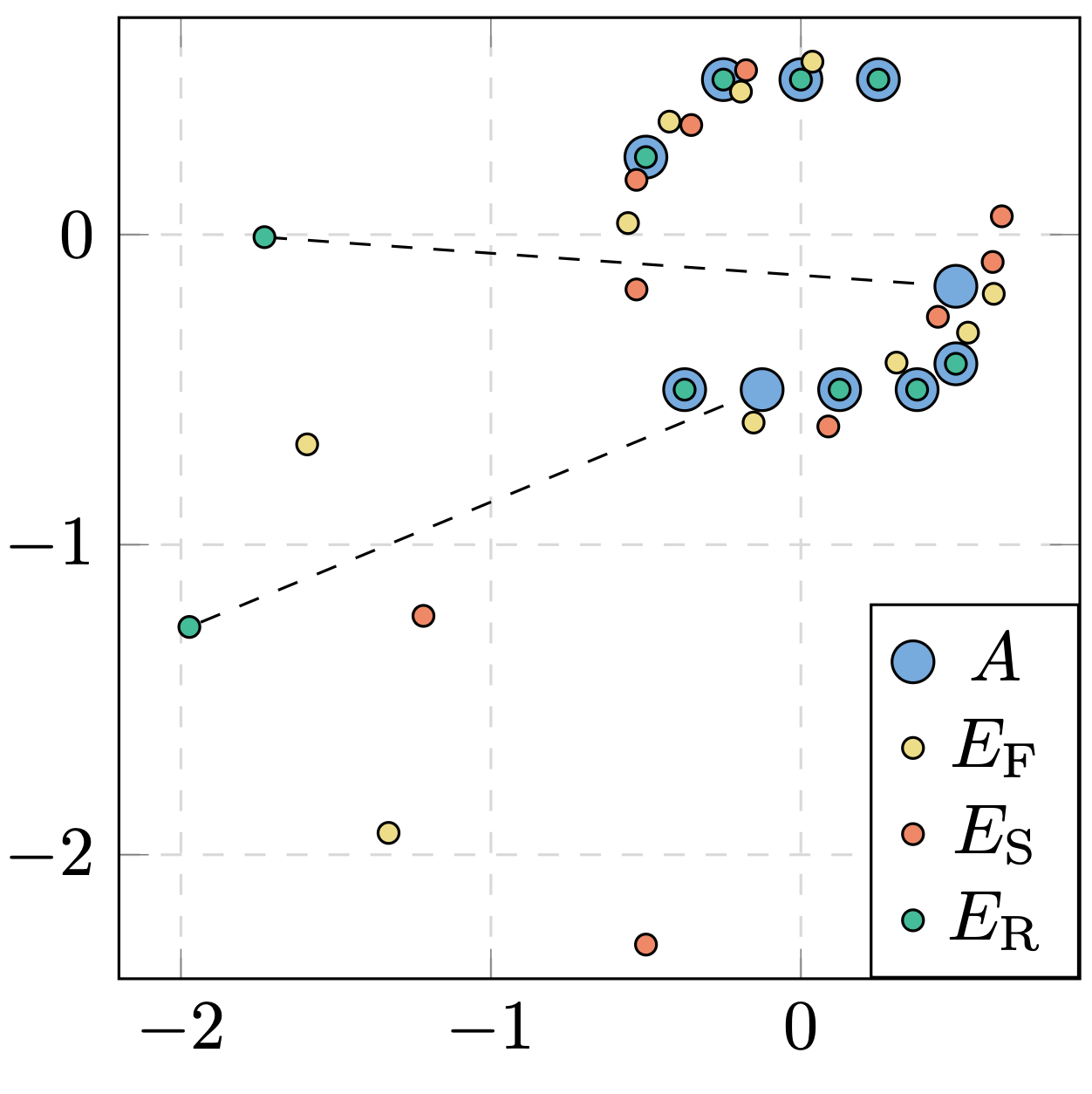
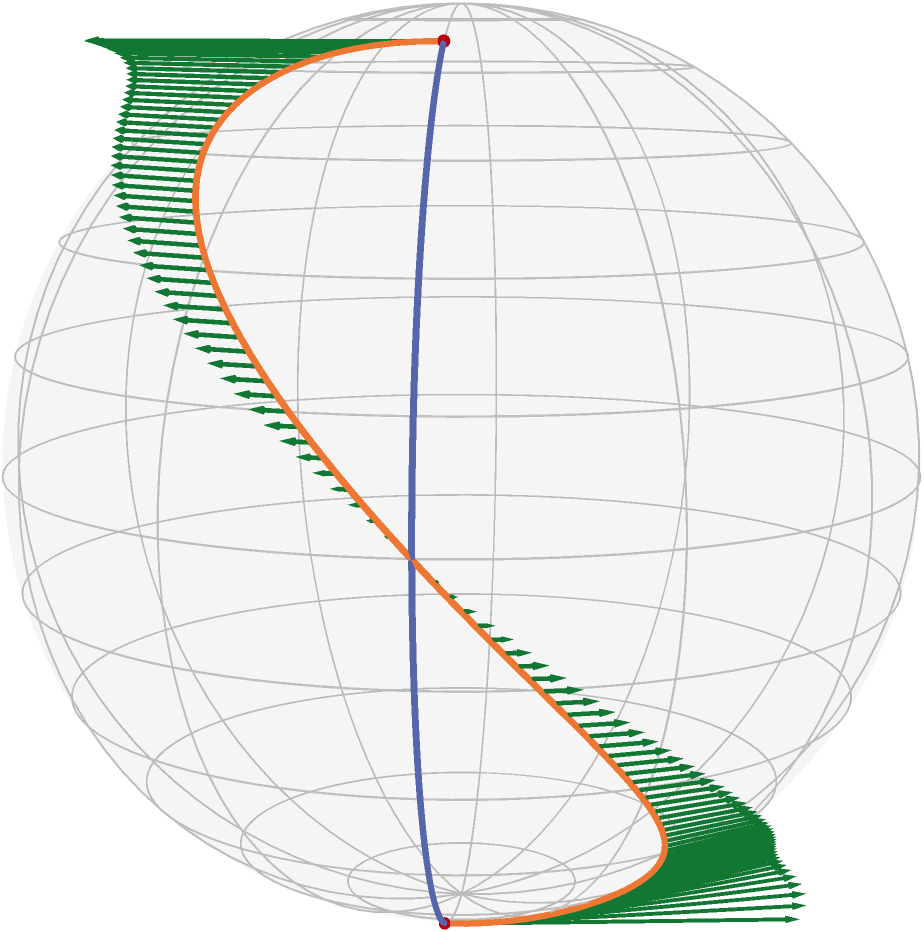
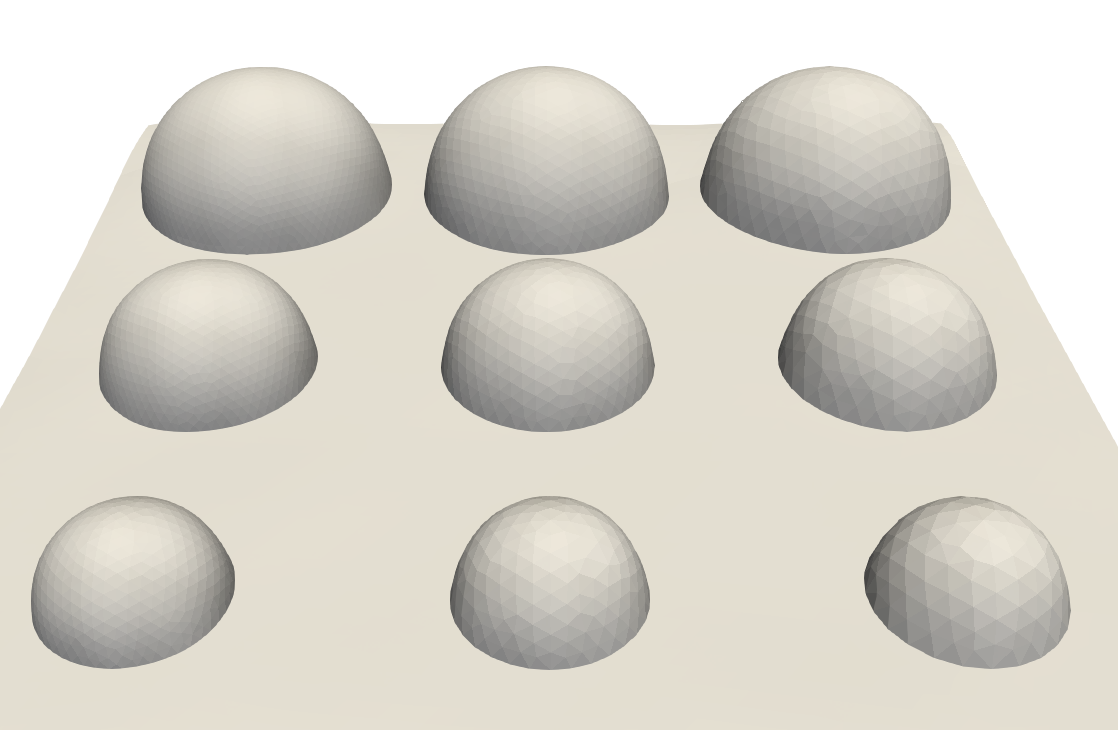
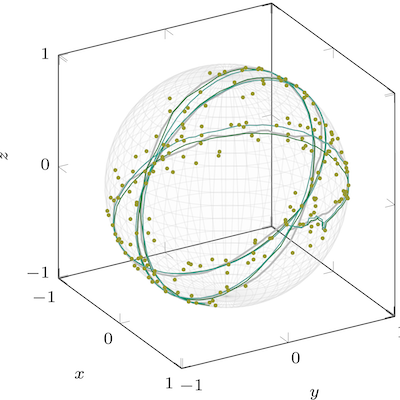
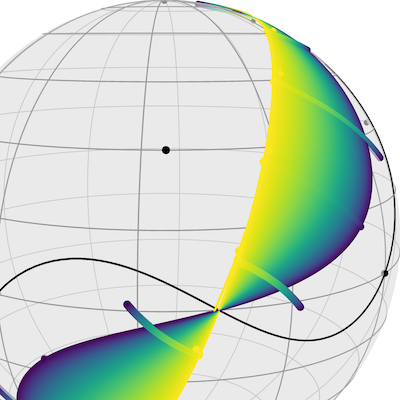
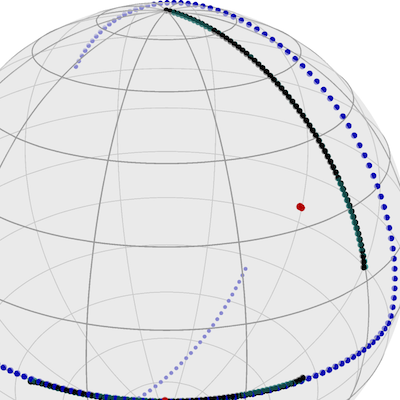
Meaningful comparison between sets of observations often necessitates alignment or registration between them, and the resulting optimization problems range in complexity from those admitting simple closed-form solutions to those requiring advanced and novel techniques. We compare different Procrustes problems in which we align two sets of points after various perturbations by minimizing the norm of the difference between one matrix and an orthogonal transformation of the other. The minimization problem depends significantly on the choice of matrix norm; we highlight recent developments in nonsmooth Riemannian optimization and characterize which choices of norm work best for each perturbation. We show that in several applications, from low-dimensional alignments to hypothesis testing for random networks, when Procrustes alignment with the spectral or robust norm is the appropriate choice, it is often feasible to replace the computationally more expensive spectral and robust minimizers with their closed-form Frobenius-norm counterpart. Our work reinforces the synergy between optimization, geometry, and statistics.
Publications
-
Jasa, H., Bergmann, R., Kümmerle, C., Athreya, A., Lubberts, Z.2025Procrustes Problems on Random Matrices
arxiv 2510.05182@online{JasaBergmannKuemmerleAthreyaLubberts-2025, eprint = {2510.05182}, author = {Jasa, H. and Bergmann, R. and Kümmerle, C. and Athreya, A. and Lubberts, Z.}, eprinttype = {arxiv}, title = {Procrustes Problems on Random Matrices}, abstract = { Meaningful comparison between sets of observations often necessitates alignment or registration between them, and the resulting optimization problems range in complexity from those admitting simple closed-form solutions to those requiring advanced and novel techniques. We compare different Procrustes problems in which we align two sets of points after various perturbations by minimizing the norm of the difference between one matrix and an orthogonal transformation of the other. The minimization problem depends significantly on the choice of matrix norm; we highlight recent developments in nonsmooth Riemannian optimization and characterize which choices of norm work best for each perturbation. We show that in several applications, from low-dimensional alignments to hypothesis testing for random networks, when Procrustes alignment with the spectral or robust norm is the appropriate choice, it is often feasible to replace the computationally more expensive spectral and robust minimizers with their closed-form Frobenius-norm counterpart. Our work reinforces the synergy between optimization, geometry, and statistics. }, year = {2025}, } -
Bergmann, R., Jasa, H., John, P., Pfeffer, M.2025The Intrinsic Riemannian Proximal Gradient Method for Convex Optimization
arxiv 2507.16055We consider a class of (possibly strongly) geodesically convex optimization problems on Hadamard manifolds, where the objective function splits into the sum of a smooth and a possibly nonsmooth function. We introduce an intrinsic convex Riemannian proximal gradient (CRPG) method that employs the manifold proximal map for the nonsmooth step, without operating in the embedding or tangent space. A sublinear convergence rate for convex problems and a linear convergence rate for strongly convex problems is established, and we derive fundamental proximal gradient inequalities that generalize the Euclidean case. Our numerical experiments on hyperbolic spaces and manifolds of symmetric positive definite matrices demonstrate substantial computational advantages over existing methods.
@online{BergmannJasaJohnPfeffer-2025b, eprint = {2507.16055}, author = {Bergmann, R. and Jasa, H. and John, P. and Pfeffer, M.}, year = {2025}, eprinttype = {arxiv}, title = {The Intrinsic Riemannian Proximal Gradient Method for Convex Optimization}, abstract = { We consider a class of (possibly strongly) geodesically convex optimization problems on Hadamard manifolds, where the objective function splits into the sum of a smooth and a possibly nonsmooth function. We introduce an intrinsic convex Riemannian proximal gradient (CRPG) method that employs the manifold proximal map for the nonsmooth step, without operating in the embedding or tangent space. A sublinear convergence rate for convex problems and a linear convergence rate for strongly convex problems is established, and we derive fundamental proximal gradient inequalities that generalize the Euclidean case. Our numerical experiments on hyperbolic spaces and manifolds of symmetric positive definite matrices demonstrate substantial computational advantages over existing methods. }, } -
Weigl, L., Bergmann, R., Schiela, A.2025Newton's method for nonlinear mappings into vector bundles Part II: Application to variational problems
arxiv 2507.13836We consider the solution of variational equations on manifolds by Newton's method. These problems can be expressed as root finding problems for mappings from infinite dimensional manifolds into dual vector bundles. We derive the differential geometric tools needed for the realization of Newton's method, equipped with an affine covariant damping strategy. We apply Newton's method to a couple of variational problems and show numerical results.
@online{WeiglBergmannSchiela-2025, eprint = {2507.13836}, author = {Weigl, L. and Bergmann, R. and Schiela, A.}, year = {2025}, eprinttype = {arxiv}, title = {Newton's method for nonlinear mappings into vector bundles Part II: Application to variational problems}, abstract = { We consider the solution of variational equations on manifolds by Newton's method. These problems can be expressed as root finding problems for mappings from infinite dimensional manifolds into dual vector bundles. We derive the differential geometric tools needed for the realization of Newton's method, equipped with an affine covariant damping strategy. We apply Newton's method to a couple of variational problems and show numerical results. }, } -
Baumgärtner, L., Bergmann, R., Herzog, R., Schmidt, S., Weiß, M.2025Total Generalized Variation of the Normal Vector Field and Applications to Mesh Denoising
arxiv 2507.13530 Accepted for publication in SIAM Journal on Imaging SciencesWe propose a novel formulation for the second-order total generalized variation (TGV) of the normal vector on an oriented, triangular mesh embedded in . The normal vector is considered as a manifold-valued function, taking values on the unit sphere. Our formulation extends previous discrete TGV models for piecewise constant scalar data that utilize a Raviart-Thomas function space. To exctend this formulation to the manifold setting, a tailor-made tangential Raviart-Thomas type finite element space is constructed in this work. The new regularizer is compared to existing methods in mesh denoising experiments.
@online{BaumgaertnerBergmannHerzogSchmidtWeiss-2025, eprint = {2507.13530}, author = {Baumgärtner, L. and Bergmann, R. and Herzog, R. and Schmidt, S. and Weiß, M.}, note = {Accepted for publication in SIAM Journal on Imaging Sciences}, year = {2025}, eprinttype = {arxiv}, title = {Total Generalized Variation of the Normal Vector Field and Applications to Mesh Denoising}, abstract = { We propose a novel formulation for the second-order total generalized variation (TGV) of the normal vector on an oriented, triangular mesh embedded in $\R^3$. The normal vector is considered as a manifold-valued function, taking values on the unit sphere. Our formulation extends previous discrete TGV models for piecewise constant scalar data that utilize a Raviart-Thomas function space. To exctend this formulation to the manifold setting, a tailor-made tangential Raviart-Thomas type finite element space is constructed in this work. The new regularizer is compared to existing methods in mesh denoising experiments. }, } -
Bergmann, R., Jasa, H., John, P., Pfeffer, M.2025The Intrinsic Riemannian Proximal Gradient Method for Nonconvex Optimization
arxiv 2506.09775We consider the proximal gradient method on Riemannian manifolds for functions that are possibly not geodesically convex. Starting from the forward-backward-splitting, we define an intrinsic variant of the proximal gradient method that uses proximal maps defined on the manifold and therefore does not require or work in the embedding. We investigate its convergence properties and illustrate its numerical performance, particularly for nonconvex or nonembedded problems that are hence out of reach for other methods.
@online{BergmannJasaJohnPfeffer-2025, eprint = {2506.09775}, author = {Bergmann, R. and Jasa, H. and John, P. and Pfeffer, M.}, year = {2025}, eprinttype = {arxiv}, title = {The Intrinsic Riemannian Proximal Gradient Method for Nonconvex Optimization}, abstract = { We consider the proximal gradient method on Riemannian manifolds for functions that are possibly not geodesically convex. Starting from the forward-backward-splitting, we define an intrinsic variant of the proximal gradient method that uses proximal maps defined on the manifold and therefore does not require or work in the embedding. We investigate its convergence properties and illustrate its numerical performance, particularly for nonconvex or nonembedded problems that are hence out of reach for other methods. }, } -
Baran, M., Bergmann, R.2025A geometric perspective of state estimation using Kalman filters
arxiv 2506.01086Geometry of the state space is known to play a crucial role in many applications of Kalman filters, especially robotics and motion tracking. The Lie group-centric approach is currently very common, although a Riemannian approach has also been developed. In this work we explore the relationship between these two approaches and develop a novel description of Kalman filters based on affine connections that generalizes both commonly encountered descriptions. We illustrate the results on two test problems involving the special Euclidean group and the tangent bundle of a sphere in which the state is tracked by geometric variants of the extended Kalman filter and the unscented Kalman filter. The examples use a newly developed library
GeometricKalman.jl. The new approach provides a greater freedom in selecting the structure of the state space for state estimation and can be easily integrated with standard techniques such as parameter estimation or covariance matrix estimation.@online{BaranBergmann-2025, eprint = {2506.01086}, author = {Baran, M. and Bergmann, R.}, year = {2025}, eprinttype = {arxiv}, title = {A geometric perspective of state estimation using Kalman filters}, abstract = { Geometry of the state space is known to play a crucial role in many applications of Kalman filters, especially robotics and motion tracking. The Lie group-centric approach is currently very common, although a Riemannian approach has also been developed. In this work we explore the relationship between these two approaches and develop a novel description of Kalman filters based on affine connections that generalizes both commonly encountered descriptions. We illustrate the results on two test problems involving the special Euclidean group and the tangent bundle of a sphere in which the state is tracked by geometric variants of the extended Kalman filter and the unscented Kalman filter. The examples use a newly developed library [`GeometricKalman.jl`](https://github.com/JuliaManifolds/GeometricKalman.jl). The new approach provides a greater freedom in selecting the structure of the state space for state estimation and can be easily integrated with standard techniques such as parameter estimation or covariance matrix estimation. }, } -
Baumgärtner, L., Bergmann, R., Herzog, R., Schmidt, S., Weiß, M.2024Two Models for Surface Segmentation using the Total Variation of the Normal Vector
arxiv 2412.00445We consider the problem of surface segmentation, where the goal is to partition a surface represented by a triangular mesh. The segmentation is based on the similarity of the normal vector field to a given set of label vectors. We propose a variational approach and compare two different regularizers, both based on a total variation measure. The first regularizer penalizes the total variation of the assignment function directly, while the second regularizer penalizes the total variation in the label space. In order to solve the resulting optimization problems, we use variations of the split Bregman (ADMM) iteration adapted to the problem at hand. While computationally more expensive, the second regularizer yields better results in our experiments, in particular it removes noise more reliably in regions of constant curvature.
@online{BaumgärtnerBergmannHerzogSchmidtWeiß-2024, eprint = {2412.00445}, author = {Baumgärtner, L. and Bergmann, R. and Herzog, R. and Schmidt, S. and Weiß, M.}, year = {2024}, eprinttype = {arxiv}, title = {Two Models for Surface Segmentation using the Total Variation of the Normal Vector}, abstract = { We consider the problem of surface segmentation, where the goal is to partition a surface represented by a triangular mesh. The segmentation is based on the similarity of the normal vector field to a given set of label vectors. We propose a variational approach and compare two different regularizers, both based on a total variation measure. The first regularizer penalizes the total variation of the assignment function directly, while the second regularizer penalizes the total variation in the label space. In order to solve the resulting optimization problems, we use variations of the split Bregman (ADMM) iteration adapted to the problem at hand. While computationally more expensive, the second regularizer yields better results in our experiments, in particular it removes noise more reliably in regions of constant curvature. }, } -
Schiela, A., Herzog, R., Bergmann, R.2024Nonlinear Fenchel conjugates
arxiv 2409.04492The classical concept of Fenchel conjugation is tailored to extended real-valued functions defined on linear spaces. In this paper we generalize this concept to functions defined on arbitrary sets that do not necessarily bear any structure at all. This generalization is obtained by replacing linear test functions by general nonlinear ones. Thus, we refer to it as nonlinear Fenchel conjugation. We investigate elementary properties including the Fenchel-Moreau biconjugation theorem. Whenever the domain exhibits additional structure, the restriction to a suitable subset of test functions allows further results to be derived. For example, on smooth manifolds, the restriction to smooth test functions allows us to state the Fenchel-Young theorem for the viscosity Fréchet subdifferential. On Lie groups, the restriction to real-valued group homomorphisms relates nonlinear Fenchel conjugation to infimal convolution and yields a notion of convexity.
@online{SchielaHerzogBergmann-2024, eprint = {2409.04492}, author = {Schiela, A. and Herzog, R. and Bergmann, R.}, year = {2024}, eprinttype = {arxiv}, title = {Nonlinear Fenchel conjugates}, abstract = { The classical concept of Fenchel conjugation is tailored to extended real-valued functions defined on linear spaces. In this paper we generalize this concept to functions defined on arbitrary sets that do not necessarily bear any structure at all. This generalization is obtained by replacing linear test functions by general nonlinear ones. Thus, we refer to it as nonlinear Fenchel conjugation. We investigate elementary properties including the Fenchel-Moreau biconjugation theorem. Whenever the domain exhibits additional structure, the restriction to a suitable subset of test functions allows further results to be derived. For example, on smooth manifolds, the restriction to smooth test functions allows us to state the Fenchel-Young theorem for the viscosity Fréchet subdifferential. On Lie groups, the restriction to real-valued group homomorphisms relates nonlinear Fenchel conjugation to infimal convolution and yields a notion of convexity. }, } -
Bergmann, R., Herzog, R., Jasa, H.2024The Riemannian Convex Bundle Method
arxiv 2402.13670We introduce the convex bundle method to solve convex, non-smooth optimization problems on Riemannian manifolds. Each step of our method is based on a model that involves the convex hull of previously collected subgradients, parallely transported into the current serious iterate. This approach generalizes the dual form of classical bundle subproblems in Euclidean space. We prove that, under mild conditions, the convex bundle method converges to a minimizer. Several numerical examples implemented using the Julia package
Manopt.jlillustrate the performance of the proposed method and compare it to the subgradient method, the cyclic proximal point, as well as the proximal bundle algorithm from Hoseini Monjezi, Nobakhtian, Pouryayevali, 2021.@online{BergmannHerzogJasa-2024, eprint = {2402.13670}, author = {Bergmann, R. and Herzog, R. and Jasa, H.}, year = {2024}, eprinttype = {arxiv}, title = {The Riemannian Convex Bundle Method}, abstract = { We introduce the convex bundle method to solve convex, non-smooth optimization problems on Riemannian manifolds. Each step of our method is based on a model that involves the convex hull of previously collected subgradients, parallely transported into the current serious iterate. This approach generalizes the dual form of classical bundle subproblems in Euclidean space. We prove that, under mild conditions, the convex bundle method converges to a minimizer. Several numerical examples implemented using the Julia package [`Manopt.jl`](https://manoptjl.org) illustrate the performance of the proposed method and compare it to the subgradient method, the cyclic proximal point, as well as the proximal bundle algorithm from [Hoseini Monjezi, Nobakhtian, Pouryayevali, 2021](https://doi.org/10.1093/imanum/drab091). }, }
Preprints
Journal Articles
-
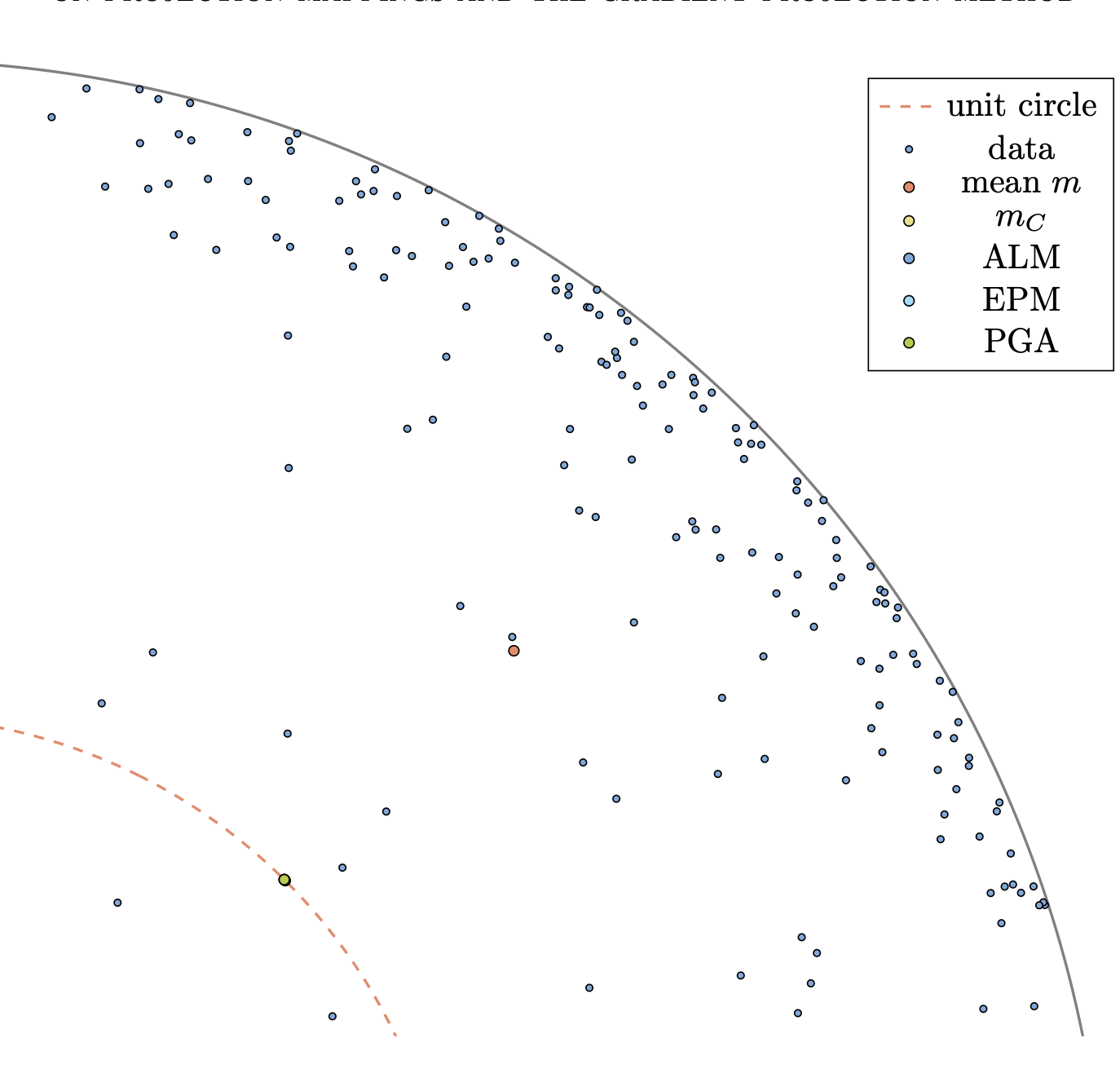
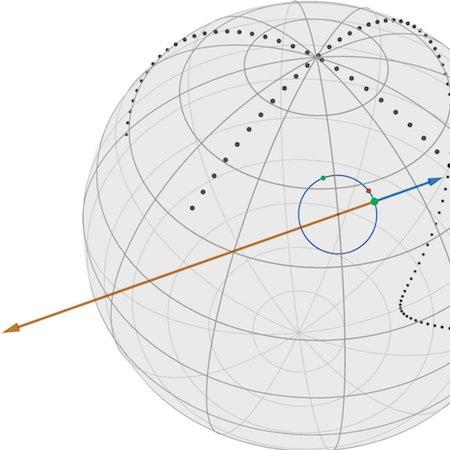
Bergmann, R., Ferreira, O. P., Németh, S. Z., Zhu, J.2025On projection mappings and the gradient projection method on hyperbolic space forms
IMA Journal of Numerical Analysisdraf097This paper presents several new properties of the intrinsic -projection into -hyperbolically convex sets of -hyperbolic space forms, along with closed-form formulas for the intrinsic -projection into specific -hyperbolically convex sets. It also discusses the relationship between the intrinsic -projection, the Euclidean orthogonal projection, and the Lorentz projection. These properties lay the groundwork for analyzing the gradient projection method and hold importance in their own right. Additionally, new properties of the gradient projection method to solve constrained optimization problems in -hyperbolic space forms are established, considering both constant and backtracking step sizes in the analysis. It is shown that every accumulation point of the sequence generated by the method for both step sizes is a stationary point for the given problem. Additionally, an iteration complexity bound is provided that upper bounds the number of iterations needed to achieve a suitable measure of stationarity for both step sizes. Finally, the properties of the constrained Fermat-Weber problem are explored, demonstrating that the sequence generated by the gradient projection method converges to its unique solution. Numerical experiments on solving the Fermat-Weber problem are presented, illustrating the theoretical findings and demonstrating the effectiveness of the proposed methods.
@article{BergmannFerreiraNemethZhu-2025, pages = {draf097}, doi = {10.1093/imanum/draf097}, author = {Bergmann, R. and Ferreira, O. P. and Németh, S. Z. and Zhu, J.}, eprint = {2504.11815}, year = {2025}, eprinttype = {arxiv}, journaltitle = {IMA Journal of Numerical Analysis}, title = {On projection mappings and the gradient projection method on hyperbolic space forms}, abstract = { This paper presents several new properties of the intrinsic $\kappa$-projection into $\kappa$-hyperbolically convex sets of $\kappa$-hyperbolic space forms, along with closed-form formulas for the intrinsic $\kappa$-projection into specific $\kappa$-hyperbolically convex sets. It also discusses the relationship between the intrinsic $\kappa$-projection, the Euclidean orthogonal projection, and the Lorentz projection. These properties lay the groundwork for analyzing the gradient projection method and hold importance in their own right. Additionally, new properties of the gradient projection method to solve constrained optimization problems in $\kappa$-hyperbolic space forms are established, considering both constant and backtracking step sizes in the analysis. It is shown that every accumulation point of the sequence generated by the method for both step sizes is a stationary point for the given problem. Additionally, an iteration complexity bound is provided that upper bounds the number of iterations needed to achieve a suitable measure of stationarity for both step sizes. Finally, the properties of the constrained Fermat-Weber problem are explored, demonstrating that the sequence generated by the gradient projection method converges to its unique solution. Numerical experiments on solving the Fermat-Weber problem are presented, illustrating the theoretical findings and demonstrating the effectiveness of the proposed methods. }, } -
Baumgärtner, L., Bergmann, R., Herzog, R., Schmidt, S., Vidal-Núñez, J., Weiß, M.2025Mesh Denoising and Inpainting using the Total Variation of the Normal and a Shape Newton Approach
SIAM Journal on Scientific Computing471A300–A324We present a novel approach to denoising and inpainting problems for surface meshes. The purpose of these problems is to remove noise or fill in missing parts while preserving important features such as sharp edges. A discrete variant of the total variation of the unit normal vector field serves as a regularizing functional to achieve these goals. In order to solve the resulting problem, we use a version of the split Bregman (ADMM) iteration adapted to the problem. A new formulation of the total variation regularizer, as well as the use of an inexact Newton method for the shape optimization step, bring significant speed-up compared to earlier methods. Numerical examples are included, demonstrating the performance of our algorithm with some complex 3D geometries.
@article{BaumgärtnerBergmannHerrmannHerzogSchmidtVidal-Nunez-2025, issue = {1}, pages = {A300–A324}, publication-date = {2025-01-31}, doi = {10.1137/24M1646121}, author = {Baumgärtner, L. and Bergmann, R. and Herzog, R. and Schmidt, S. and Vidal-Núñez, J. and Weiß, M.}, eprint = {2012.11748}, year = {2025}, eprinttype = {arXiv}, volume = {47}, journaltitle = {SIAM Journal on Scientific Computing}, title = {Mesh Denoising and Inpainting using the Total Variation of the Normal and a Shape Newton Approach}, abstract = { We present a novel approach to denoising and inpainting problems for surface meshes. The purpose of these problems is to remove noise or fill in missing parts while preserving important features such as sharp edges. A discrete variant of the total variation of the unit normal vector field serves as a regularizing functional to achieve these goals. In order to solve the resulting problem, we use a version of the split Bregman (ADMM) iteration adapted to the problem. A new formulation of the total variation regularizer, as well as the use of an inexact Newton method for the shape optimization step, bring significant speed-up compared to earlier methods. Numerical examples are included, demonstrating the performance of our algorithm with some complex 3D geometries. }, } -
Zimmermann, R., Bergmann, R.2024Multivariate Hermite Interpolation on Riemannian Manifolds
SIAM Journal on Scientific Computing462A1276–A1297In this paper, we propose two methods for multivariate Hermite interpolation of manifold-valued functions. On the one hand, we approach the problem via for Hermite interpolation, the sampled derivative information is converted into a condition on the derivatives of the associated weight functions. It turns out that this requires the solution of linear systems of equations, but no vector transport is necessary. This approach treats all given sample data points equally and is intrinsic in the sense that it does not depend on local coordinates or embeddings. As an alternative, we consider Hermite interpolation in a tangent space. This is a straightforward approach, where one designated point, for example one of the sample points or (one of) their center(s) of mass, is chosen to act as the base point at which the tangent space is attached. The remaining sampled locations and sampled derivatives are mapped to said tangent space. This requires a vector transport between different tangent spaces. The actual interpolation is then conducted via classical vector space operations. The interpolant depends on the selected base point. The validity and performance of both approaches is illustrated by means of numerical examples.
@article{ZimmermannBergmann-2024, number = {2}, pages = {A1276–A1297}, doi = {10.1137/22M1541071}, author = {Zimmermann, R. and Bergmann, R.}, eprint = {2212.07281}, year = {2024}, eprinttype = {arXiv}, volume = {46}, journaltitle = {SIAM Journal on Scientific Computing}, title = {Multivariate Hermite Interpolation on Riemannian Manifolds}, abstract = { In this paper, we propose two methods for multivariate Hermite interpolation of manifold-valued functions. On the one hand, we approach the problem via for Hermite interpolation, the sampled derivative information is converted into a condition on the derivatives of the associated weight functions. It turns out that this requires the solution of linear systems of equations, but no vector transport is necessary. This approach treats all given sample data points equally and is intrinsic in the sense that it does not depend on local coordinates or embeddings. As an alternative, we consider Hermite interpolation in a tangent space. This is a straightforward approach, where one designated point, for example one of the sample points or (one of) their center(s) of mass, is chosen to act as the base point at which the tangent space is attached. The remaining sampled locations and sampled derivatives are mapped to said tangent space. This requires a vector transport between different tangent spaces. The actual interpolation is then conducted via classical vector space operations. The interpolant depends on the selected base point. The validity and performance of both approaches is illustrated by means of numerical examples. }, } -
Bergmann, R., Ferreira, O. P., Santos, E. M., Souza, J. C. O.2024The difference of convex algorithm on Hadamard manifolds
Journal of Optimization Theory and Applications2011221-251In this paper, we propose a Riemannian version of the difference of convex algorithm (DCA) to solve a minimization problem involving the difference of convex (DC) function. We establish the equivalence between the classical and simplified Riemannian versions of the DCA. We also prove that, under mild assumptions, the Riemannian version of the DCA is well-defined, and every cluster point of the sequence generated by the proposed method, if any, is a critical point of the objective DC function. Additionally, we establish some duality relations between the DC problem and its dual. To illustrate the effectiveness of the algorithm, we present some numerical experiments.
@article{BergmannFerreiraSantosSouza-2024, number = {1}, publication-date = {2024-02-26}, pages = {221-251}, doi = {10.1007/s10957-024-02392-8}, author = {Bergmann, R. and Ferreira, O. P. and Santos, E. M. and Souza, J. C. O.}, eprint = {2112.05250}, year = {2024}, eprinttype = {arXiv}, volume = {201}, journaltitle = {Journal of Optimization Theory and Applications}, title = {The difference of convex algorithm on Hadamard manifolds}, abstract = { In this paper, we propose a Riemannian version of the difference of convex algorithm (DCA) to solve a minimization problem involving the difference of convex (DC) function. We establish the equivalence between the classical and simplified Riemannian versions of the DCA. We also prove that, under mild assumptions, the Riemannian version of the DCA is well-defined, and every cluster point of the sequence generated by the proposed method, if any, is a critical point of the objective DC function. Additionally, we establish some duality relations between the DC problem and its dual. To illustrate the effectiveness of the algorithm, we present some numerical experiments. }, } -
Axen, S. D., Baran, M., Bergmann, R., Rzecki, K.2023Manifolds.jl: An Extensible Julia Framework for Data Analysis on Manifolds
ACM Transactions on Mathematical Software494We present the Julia package Manifolds.jl, providing a fast and easy-to-use library of Riemannian manifolds and Lie groups. This package enables working with data defined on a Riemannian manifold, such as the circle, the sphere, symmetric positive definite matrices, or one of the models for hyperbolic spaces. We introduce a common interface, available in ManifoldsBase.jl, with which new manifolds, applications, and algorithms can be implemented. We demonstrate the utility of Manifolds.jl using Bézier splines, an optimization task on manifolds, and principal component analysis on nonlinear data. In a benchmark, Manifolds.jl outperforms all comparable packages for low-dimensional manifolds in speed; over Python and Matlab packages, the improvement is often several orders of magnitude, while over C/C++ packages, the improvement is two-fold. For high-dimensional manifolds, it outperforms all packages except for Tensorflow-Riemopt, which is specifically tailored for high-dimensional manifolds.
@article{AxenBaranBergmannRzecki-2023, number = {4}, doi = {10.1145/3618296}, author = {Axen, S. D. and Baran, M. and Bergmann, R. and Rzecki, K.}, eprint = {2106.08777}, year = {2023}, eprinttype = {arXiv}, volume = {49}, journaltitle = {ACM Transactions on Mathematical Software}, title = {Manifolds.jl: An Extensible Julia Framework for Data Analysis on Manifolds}, abstract = { We present the Julia package Manifolds.jl, providing a fast and easy-to-use library of Riemannian manifolds and Lie groups. This package enables working with data defined on a Riemannian manifold, such as the circle, the sphere, symmetric positive definite matrices, or one of the models for hyperbolic spaces. We introduce a common interface, available in ManifoldsBase.jl, with which new manifolds, applications, and algorithms can be implemented. We demonstrate the utility of Manifolds.jl using Bézier splines, an optimization task on manifolds, and principal component analysis on nonlinear data. In a benchmark, Manifolds.jl outperforms all comparable packages for low-dimensional manifolds in speed; over Python and Matlab packages, the improvement is often several orders of magnitude, while over C/C++ packages, the improvement is two-fold. For high-dimensional manifolds, it outperforms all packages except for Tensorflow-Riemopt, which is specifically tailored for high-dimensional manifolds. }, } -
Baumgärtner, L., Bergmann, R., Herzog, R., Schmidt, S., Vidal-Núñez, J.2023Total Generalized Variation for Piecewise Constant Functions with Applications in Imaging
SIAM Journal on Imaging Sciences161313-339We propose a novel discrete concept for the total generalized variation (TGV), which has originally been derived to reduce the staircasing effect in classical total variation (TV) regularization, in image denoising problems. We describe discrete, second-order TGV for piecewise constant functions on triangular meshes, thus allowing the TGV functional to be applied to more general data structures than pixel images, and in particular in the context of finite element discretizations. Particular attention is given to the description of the kernel of the TGV functional, which, in the continuous setting, consists of linear polynomials. We discuss how to take advantage of this kernel structure using piecewise constant functions on triangular meshes. Numerical experiments include denoising and inpainting problems for images defined on non-standard grids, including data from a 3D scanner.
@article{BaumgärtnerBergmannHerzogSchmidtVidal-Nunez-2022, issue = {1}, pages = {313-339}, doi = {10.1137/22M1505281}, author = {Baumgärtner, L. and Bergmann, R. and Herzog, R. and Schmidt, S. and Vidal-Núñez, J.}, eprint = {2206.12331}, year = {2023}, eprinttype = {arXiv}, volume = {16}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {Total Generalized Variation for Piecewise Constant Functions with Applications in Imaging}, abstract = { We propose a novel discrete concept for the total generalized variation (TGV), which has originally been derived to reduce the staircasing effect in classical total variation (TV) regularization, in image denoising problems. We describe discrete, second-order TGV for piecewise constant functions on triangular meshes, thus allowing the TGV functional to be applied to more general data structures than pixel images, and in particular in the context of finite element discretizations. Particular attention is given to the description of the kernel of the TGV functional, which, in the continuous setting, consists of linear polynomials. We discuss how to take advantage of this kernel structure using piecewise constant functions on triangular meshes. Numerical experiments include denoising and inpainting problems for images defined on non-standard grids, including data from a 3D scanner. }, } -
Bergmann, R., Herzog, R., Ortiz López, J., Schiela, A.2022First- and Second-Order Analysis for Optimization Problems with Manifold-Valued Constraints
Journal of Optimization Theory and ApplicationsWe consider optimization problems with manifold-valued constraints. These generalize classical equality and inequality constraints to a setting in which both the domain and the codomain of the constraint mapping are smooth manifolds. We model the feasible set as the preimage of a submanifold with corners of the codomain. The latter is a subset which corresponds to a convex cone locally in suitable charts. We study first- and second-order optimality conditions for this class of problems. We also show the invariance of the relevant quantities with respect to local representations of the problem.
@article{BergmannHerzogOrtizLopezSchiela-2022, doi = {10.1007/s10957-022-02107-x}, author = {Bergmann, R. and Herzog, R. and Ortiz López, J. and Schiela, A.}, eprint = {2110.04882}, year = {2022}, eprinttype = {arXiv}, journaltitle = {Journal of Optimization Theory and Applications}, title = {First- and Second-Order Analysis for Optimization Problems with Manifold-Valued Constraints}, abstract = { We consider optimization problems with manifold-valued constraints. These generalize classical equality and inequality constraints to a setting in which both the domain and the codomain of the constraint mapping are smooth manifolds. We model the feasible set as the preimage of a submanifold with corners of the codomain. The latter is a subset which corresponds to a convex cone locally in suitable charts. We study first- and second-order optimality conditions for this class of problems. We also show the invariance of the relevant quantities with respect to local representations of the problem. }, } -
Silva Louzeiro, M., Bergmann, R., Herzog, R.2022Fenchel Duality and a Separation Theorem on Hadamard Manifolds
SIAM Journal on Optimization322854-873In this paper, we introduce a definition of Fenchel conjugate and Fenchel biconjugate on Hadamard manifolds based on the tangent bundle. Our definition overcomes the inconvenience that the conjugate depends on the choice of a certain point on the manifold, as previous definitions required. On the other hand, this new definition still possesses properties known to hold in the Euclidean case. It even yields a broader interpretation of the Fenchel conjugate in the Euclidean case itself. Most prominently, our definition of the Fenchel conjugate provides a Fenchel-Moreau Theorem for geodesically convex, proper, lower semicontinuous functions. In addition, this framework allows us to develop a theory of separation of convex sets on Hadamard manifolds, and a strict separation theorem is obtained.
@article{SilvaLouzeiroBergmannHerzog-2022, number = {2}, pages = {854-873}, doi = {10.1137/21M1400699}, author = {Silva Louzeiro, M. and Bergmann, R. and Herzog, R.}, eprint = {2102.11155}, year = {2022}, eprinttype = {arXiv}, volume = {32}, journaltitle = {SIAM Journal on Optimization}, title = {{F}enchel Duality and a Separation Theorem on Hadamard Manifolds}, abstract = { In this paper, we introduce a definition of Fenchel conjugate and Fenchel biconjugate on Hadamard manifolds based on the tangent bundle. Our definition overcomes the inconvenience that the conjugate depends on the choice of a certain point on the manifold, as previous definitions required. On the other hand, this new definition still possesses properties known to hold in the Euclidean case. It even yields a broader interpretation of the Fenchel conjugate in the Euclidean case itself. Most prominently, our definition of the Fenchel conjugate provides a Fenchel-Moreau Theorem for geodesically convex, proper, lower semicontinuous functions. In addition, this framework allows us to develop a theory of separation of convex sets on Hadamard manifolds, and a strict separation theorem is obtained. }, } -
Bergmann, R.2022Manopt.jl: Optimization on Manifolds in Julia
Journal of Open Source Software7703866, The Open JournalManopt.jlprovides a set of optimization algorithms for optimization problems given on a Riemannian manifold . Based on a generic optimization framework, together with the interfaceManifoldsBase.jlfor Riemannian manifolds, classical and recently developed methods are provided in an efficient implementation. Algorithms include the derivative-free Particle Swarm and Nelder–Mead algorithms, as well as classical gradient, conjugate gradient and stochastic gradient descent. Furthermore, quasi-Newton methods like a Riemannian L-BFGS and nonsmooth optimization algorithms like a Cyclic Proximal Point Algorithm, a (parallel) Douglas-Rachford algorithm and a Chambolle-Pock algorithm are provided, together with several basic cost functions, gradients and proximal maps as well as debug and record capabilities.@article{Bergmann-2022, publisher = {The Open Journal}, pdf = {https://www.theoj.org/joss-papers/joss.03866/10.21105.joss.03866.pdf}, number = {70}, pages = {3866}, doi = {10.21105/joss.03866}, author = {Bergmann, R.}, year = {2022}, volume = {7}, journaltitle = {Journal of Open Source Software}, title = {Manopt.jl: Optimization on Manifolds in Julia}, abstract = { [`Manopt.jl`](https://manoptjl.org) provides a set of optimization algorithms for optimization problems given on a Riemannian manifold $\mathcal M$. Based on a generic optimization framework, together with the interface [`ManifoldsBase.jl`](https://github.com/JuliaManifolds/ManifoldsBase.jl) for Riemannian manifolds, classical and recently developed methods are provided in an efficient implementation. Algorithms include the derivative-free Particle Swarm and Nelder–Mead algorithms, as well as classical gradient, conjugate gradient and stochastic gradient descent. Furthermore, quasi-Newton methods like a Riemannian L-BFGS and nonsmooth optimization algorithms like a Cyclic Proximal Point Algorithm, a (parallel) Douglas-Rachford algorithm and a Chambolle-Pock algorithm are provided, together with several basic cost functions, gradients and proximal maps as well as debug and record capabilities. }, } -
Bergmann, R., Herzog, R., Silva Louzeiro, M., Tenbrinck, T., Vidal-Núñez, J.2021Fenchel duality for Convex Optimization and a Primal Dual Algorithm on Riemannian Manifolds
Foundations of Computational MathematicsIn this paper, we introduce a definition of Fenchel conjugate and Fenchel biconjugate on Hadamard manifolds based on the tangent bundle. Our definition overcomes the inconvenience that the conjugate depends on the choice of a certain point on the manifold, as previous definitions required. On the other hand, this new definition still possesses properties known to hold in the Euclidean case. The tangent bundle approach even yields a broader interpretation of the Fenchel conjugate in the Euclidean case itself. Most prominently, our definition of the Fenchel conjugate provides a Fenchel-Moreau Theorem for geodesically convex, proper, lower semicontinuous functions. In addition, this framework allows us to develop a theory of separation of convex sets on Hadamard manifolds, and we obtain a strict separation theorem.
@article{BergmannHerzogSilvaLouzeiroTenbrinckVidal-Nunez-2021, doi = {10.1007/s10208-020-09486-5}, author = {Bergmann, R. and Herzog, R. and Silva Louzeiro, M. and Tenbrinck, T. and Vidal-Núñez, J.}, eprint = {1908.02022}, year = {2021}, eprinttype = {arXiv}, journaltitle = {Foundations of Computational Mathematics}, title = {{F}enchel duality for Convex Optimization and a Primal Dual Algorithm on {R}iemannian Manifolds}, abstract = { In this paper, we introduce a definition of Fenchel conjugate and Fenchel biconjugate on Hadamard manifolds based on the tangent bundle. Our definition overcomes the inconvenience that the conjugate depends on the choice of a certain point on the manifold, as previous definitions required. On the other hand, this new definition still possesses properties known to hold in the Euclidean case. The tangent bundle approach even yields a broader interpretation of the Fenchel conjugate in the Euclidean case itself. Most prominently, our definition of the Fenchel conjugate provides a Fenchel-Moreau Theorem for geodesically convex, proper, lower semicontinuous functions. In addition, this framework allows us to develop a theory of separation of convex sets on Hadamard manifolds, and we obtain a strict separation theorem. }, } -
Bergmann, R., Herrmann, M., Herzog, R., Schmidt, S., Vidal-Núñez, J.2020Discrete total variation of the normal vector field as shape prior with applications in geometric inverse problems
Inverse Problems365054003An analogue of the total variation prior for the normal vector field along the boundary of piecewise flat shapes in 3D is introduced. A major class of examples are triangulated surfaces as they occur for instance in finite element computations. The analysis of the functional is based on a differential geometric setting in which the unit normal vector is viewed as an element of the two-dimensional sphere manifold. It is found to agree with the discrete total mean curvature known in discrete differential geometry. A split Bregman iteration is proposed for the solution of discretized shape optimization problems, in which the total variation of the normal appears as a regularizer. Unlike most other priors, such as surface area, the new functional allows for piecewise flat shapes. As two applications, a mesh denoising and a geometric inverse problem of inclusion detection type involving a partial differential equation are considered. Numerical experiments confirm that polyhedral shapes can be identified quite accurately.
@article{BergmannHerrmannHerzogSchmidtVidal-Nunez-2020-2, number = {5}, pages = {054003}, doi = {10.1088/1361-6420/ab6d5c}, author = {Bergmann, R. and Herrmann, M. and Herzog, R. and Schmidt, S. and Vidal-Núñez, J.}, eprint = {1908.07916}, year = {2020}, eprinttype = {arXiv}, volume = {36}, journaltitle = {Inverse Problems}, title = {Discrete total variation of the normal vector field as shape prior with applications in geometric inverse problems}, abstract = { An analogue of the total variation prior for the normal vector field along the boundary of piecewise flat shapes in 3D is introduced. A major class of examples are triangulated surfaces as they occur for instance in finite element computations. The analysis of the functional is based on a differential geometric setting in which the unit normal vector is viewed as an element of the two-dimensional sphere manifold. It is found to agree with the discrete total mean curvature known in discrete differential geometry. A split Bregman iteration is proposed for the solution of discretized shape optimization problems, in which the total variation of the normal appears as a regularizer. Unlike most other priors, such as surface area, the new functional allows for piecewise flat shapes. As two applications, a mesh denoising and a geometric inverse problem of inclusion detection type involving a partial differential equation are considered. Numerical experiments confirm that polyhedral shapes can be identified quite accurately. }, } -
Bergmann, R., Herrmann, M., Herzog, R., Schmidt, S., Vidal-Núñez, J.2020Total variation of the normal vector field as shape prior
Inverse Problems365054004An analogue of the total variation prior for the normal vector field along the boundary of smooth shapes in 3D is introduced. The analysis of the total variation of the normal vector field is based on a differential geometric setting in which the unit normal vector is viewed as an element of the two-dimensional sphere manifold. It is shown that spheres are stationary points when the total variation of the normal is minimized under an area constraint. Shape calculus is used to characterize the relevant derivatives. Since the total variation functional is non-differentiable whenever the boundary contains flat regions, an extension of the split Bregman method to manifold valued functions is proposed.
@article{BergmannHerrmannHerzogSchmidtVidal-Nunez-2020-1, number = {5}, pages = {054004}, doi = {10.1088/1361-6420/ab6d5b}, author = {Bergmann, R. and Herrmann, M. and Herzog, R. and Schmidt, S. and Vidal-Núñez, J.}, eprint = {1902.0724}, year = {2020}, eprinttype = {arXiv}, volume = {36}, journaltitle = {Inverse Problems}, title = {Total variation of the normal vector field as shape prior}, abstract = { An analogue of the total variation prior for the normal vector field along the boundary of smooth shapes in 3D is introduced. The analysis of the total variation of the normal vector field is based on a differential geometric setting in which the unit normal vector is viewed as an element of the two-dimensional sphere manifold. It is shown that spheres are stationary points when the total variation of the normal is minimized under an area constraint. Shape calculus is used to characterize the relevant derivatives. Since the total variation functional is non-differentiable whenever the boundary contains flat regions, an extension of the split Bregman method to manifold valued functions is proposed. }, } -
Bergmann, R., Merkert, D.2020FFT-based homogenization on periodic anisotropic translation invariant spaces
Applied and Computational Harmonic Analysis481266–292In this paper we derive a discretisation of the equation of quasi-static elasticity in homogenization in form of a variational formulation and the so-called Lippmann-Schwinger equation, in anisotropic spaces of translates of periodic functions. We unify and extend the truncated Fourier series approach, the constant finite element ansatz and the anisotropic lattice derivation. The resulting formulation of the Lippmann-Schwinger equation in anisotropic translation invariant spaces unifies and analyses for the first time both the Fourier methods and finite element approaches in a common mathematical framework. We further define and characterize the resulting periodised Green operator. This operator coincides in case of a Dirichlet kernel corresponding to a diagonal matrix with the operator derived for the Galerkin projection stemming from the truncated Fourier series approach and to the anisotropic lattice derivation for all other Dirichlet kernels. Additionally, we proof the boundedness of the periodised Green operator. The operator further constitutes a projection if and only if the space of translates is generated by a Dirichlet kernel. Numerical examples for both the de la Vallée Poussin means and Box splines illustrate the flexibility of this framework.
@article{BergmannMerkert-2020, number = {1}, pages = {266–292}, doi = {10.1016/j.acha.2018.05.003}, author = {Bergmann, R. and Merkert, D.}, eprint = {1701.04685}, year = {2020}, eprinttype = {arXiv}, volume = {48}, journaltitle = {Applied and Computational Harmonic Analysis}, title = {{FFT}-based homogenization on periodic anisotropic translation invariant spaces}, abstract = { In this paper we derive a discretisation of the equation of quasi-static elasticity in homogenization in form of a variational formulation and the so-called Lippmann-Schwinger equation, in anisotropic spaces of translates of periodic functions. We unify and extend the truncated Fourier series approach, the constant finite element ansatz and the anisotropic lattice derivation. The resulting formulation of the Lippmann-Schwinger equation in anisotropic translation invariant spaces unifies and analyses for the first time both the Fourier methods and finite element approaches in a common mathematical framework. We further define and characterize the resulting periodised Green operator. This operator coincides in case of a Dirichlet kernel corresponding to a diagonal matrix with the operator derived for the Galerkin projection stemming from the truncated Fourier series approach and to the anisotropic lattice derivation for all other Dirichlet kernels. Additionally, we proof the boundedness of the periodised Green operator. The operator further constitutes a projection if and only if the space of translates is generated by a Dirichlet kernel. Numerical examples for both the de la Vallée Poussin means and Box splines illustrate the flexibility of this framework. }, } -
Bergmann, R., Herzog, R.2019Intrinsic formulation of KKT conditions and constraint qualifications on smooth manifolds
SIAM Journal on Optimization2942423–2444Karush-Kuhn-Tucker (KKT) conditions for equality and inequality constrained optimization problems on smooth manifolds are formulated. Under the Guignard constraint qualification, local minimizers are shown to admit Lagrange multipliers. The linear independence, Mangasarian-Fromovitz, and Abadie constraint qualifications are also formulated, and the chain “LICQ implies MFCQ implies ACQ implies GCQ” is proved. Moreover, classical connections between these constraint qualifications and the set of Lagrange multipliers are established, which parallel the results in Euclidean space. The constrained Riemannian center of mass on the sphere serves as an illustrating numerical example.
@article{BergmannHerzog-2019, number = {4}, pages = {2423–2444}, doi = {10.1137/18M1181602}, author = {Bergmann, R. and Herzog, R.}, eprint = {1804.06214}, year = {2019}, eprinttype = {arXiv}, volume = {29}, journaltitle = {SIAM Journal on Optimization}, title = {Intrinsic formulation of KKT conditions and constraint qualifications on smooth manifolds}, abstract = { Karush-Kuhn-Tucker (KKT) conditions for equality and inequality constrained optimization problems on smooth manifolds are formulated. Under the Guignard constraint qualification, local minimizers are shown to admit Lagrange multipliers. The linear independence, Mangasarian-Fromovitz, and Abadie constraint qualifications are also formulated, and the chain “LICQ implies MFCQ implies ACQ implies GCQ” is proved. Moreover, classical connections between these constraint qualifications and the set of Lagrange multipliers are established, which parallel the results in Euclidean space. The constrained Riemannian center of mass on the sphere serves as an illustrating numerical example. }, } -
Bergmann, R., Gousenbourger, P.-Y.2018A variational model for data fitting on manifolds by minimizing the acceleration of a Bézier curve
Frontiers in Applied Mathematics and StatisticsWe derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem.
@article{BergmannGousenburger-2018, doi = {10.3389/fams.2018.00059}, author = {Bergmann, R. and Gousenbourger, P.-Y.}, eprint = {1807.10090}, year = {2018}, eprinttype = {arXiv}, journaltitle = {Frontiers in Applied Mathematics and Statistics}, title = {A variational model for data fitting on manifolds by minimizing the acceleration of a {B}ézier curve}, abstract = { We derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem. }, } -
Bergmann, R., Merkert, D.2018A framework for FFT-based homogenization on anisotropic lattices
Computers & Mathematics with Applications.761125–140In order to take structural anisotropies of a given composite and different shapes of its unit cell into account, we generalize the Basic Scheme in homogenization by Moulinec and Suquet to arbitrary sampling lattices and tilings of the -dimensional Euclidean space. We employ a Fourier transform for these lattices by introducing the corresponding set of sample points, the so called pattern, and its frequency set, the generating set, both representing the anisotropy of both the shape of the unit cell and the chosen preferences in certain sampling directions. In several cases, this Fourier transform is of lower dimension than the space itself. For the so called rank--lattices it even reduces to a one-dimensional Fourier transform having the same leading coefficient as the fastest Fourier transform implementation available. We illustrate the generalized Basic Scheme on an anisotropic laminate and a generalized ellipsoidal Hashin structure. For both we give an analytical solution to the elasticity problem, in two- and three dimensions, respectively. We then illustrate the possibilities of choosing a pattern. Compared to classical grids this introduces both a reduction of computation time and a reduced error of the numerical method. It also allows for anisotropic subsampling, i.e. choosing a sub lattice of a pixel or voxel grid based on anisotropy information of the material at hand.
@article{BergmannMerkert-2018, issue = {1}, pages = {125–140}, doi = {10.1016/j.camwa.2018.04.008}, author = {Bergmann, R. and Merkert, D.}, eprint = {1605.05712}, year = {2018}, eprinttype = {arXiv}, volume = {76}, journaltitle = {Computers & Mathematics with Applications.}, title = {A framework for {FFT}-based homogenization on anisotropic lattices}, abstract = { In order to take structural anisotropies of a given composite and different shapes of its unit cell into account, we generalize the Basic Scheme in homogenization by Moulinec and Suquet to arbitrary sampling lattices and tilings of the $d$-dimensional Euclidean space. We employ a Fourier transform for these lattices by introducing the corresponding set of sample points, the so called pattern, and its frequency set, the generating set, both representing the anisotropy of both the shape of the unit cell and the chosen preferences in certain sampling directions. In several cases, this Fourier transform is of lower dimension than the space itself. For the so called rank-$1$-lattices it even reduces to a one-dimensional Fourier transform having the same leading coefficient as the fastest Fourier transform implementation available. We illustrate the generalized Basic Scheme on an anisotropic laminate and a generalized ellipsoidal Hashin structure. For both we give an analytical solution to the elasticity problem, in two- and three dimensions, respectively. We then illustrate the possibilities of choosing a pattern. Compared to classical grids this introduces both a reduction of computation time and a reduced error of the numerical method. It also allows for anisotropic subsampling, i.e. choosing a sub lattice of a pixel or voxel grid based on anisotropy information of the material at hand. }, } -
Bergmann, R., Tenbrinck, T.2018A graph framework for manifold-valued data
SIAM Journal on Imaging Sciences111325–360Graph-based methods have been proposed as a unified framework for discrete calculus of local and nonlocal image processing methods in the recent years. In order to translate variational models and partial differential equations to a graph, certain operators have been investigated and successfully applied to real-world applications involving graph models. So far the graph framework has been limited to real- and vector-valued functions on Euclidean domains. In this paper we generalize this model to the case of manifold-valued data. We introduce the basic calculus needed to formulate variational models and partial differential equations for manifold-valued functions and discuss the proposed graph framework for two particular families of operators, namely, the isotropic and anisotropic graph -Laplacian operators, . Based on the choice of we are in particular able to solve optimization problems on manifold-valued functions involving total variation () and Tikhonov () regularization. Finally, we present numerical results from processing both synthetic as well as real-world manifold-valued data, e.g., from diffusion tensor imaging (DTI) and light detection and ranging (LiDAR) data.
@article{BergmannTenbrinck-2018, issue = {1}, pages = {325–360}, doi = {10.1137/17M1118567}, author = {Bergmann, R. and Tenbrinck, T.}, eprint = {1702.05293}, year = {2018}, eprinttype = {arXiv}, volume = {11}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {A graph framework for manifold-valued data}, abstract = { Graph-based methods have been proposed as a unified framework for discrete calculus of local and nonlocal image processing methods in the recent years. In order to translate variational models and partial differential equations to a graph, certain operators have been investigated and successfully applied to real-world applications involving graph models. So far the graph framework has been limited to real- and vector-valued functions on Euclidean domains. In this paper we generalize this model to the case of manifold-valued data. We introduce the basic calculus needed to formulate variational models and partial differential equations for manifold-valued functions and discuss the proposed graph framework for two particular families of operators, namely, the isotropic and anisotropic graph $p$-Laplacian operators, $p\geq 1$. Based on the choice of $p$ we are in particular able to solve optimization problems on manifold-valued functions involving total variation ($p=1$) and Tikhonov ($p=2$) regularization. Finally, we present numerical results from processing both synthetic as well as real-world manifold-valued data, e.g., from diffusion tensor imaging (DTI) and light detection and ranging (LiDAR) data. }, } -
Bergmann, R., Fitschen, J. H., Persch, J., Steidl, G.2018Priors with coupled first and second order differences for manifold-valued image processing
Journal of Mathematical Imaging and Vision6091459–1481We generalize discrete variational models involving the infimal convolution (IC) of first and second order differences and the total generalized variation (TGV) to manifold-valued images. We propose both extrinsic and intrinsic approaches. The extrinsic models are based on embedding the manifold into an Euclidean space of higher dimension with manifold constraints. An alternating direction methods of multipliers can be employed for finding the minimizers. However, the components within the extrinsic IC or TGV decompositions live in the embedding space which makes their interpretation difficult. Therefore we investigate two intrinsic approaches: for Lie groups, we employ the group action within the models; for more general manifolds our IC model is based on recently developed absolute second order differences on manifolds, while our TGV approach uses an approximation of the parallel transport by the pole ladder. For computing the minimizers of the intrinsic models we apply gradient descent algorithms. Numerical examples demonstrate that our approaches work well for certain manifolds.
@article{BergmannFitschenPerschSteidl-2018, issue = {9}, pages = {1459–1481}, doi = {10.1007/s10851-018-0840-y}, author = {Bergmann, R. and Fitschen, J. H. and Persch, J. and Steidl, G.}, eprint = {1709.01343}, year = {2018}, eprinttype = {arXiv}, volume = {60}, journaltitle = {Journal of Mathematical Imaging and Vision}, title = {Priors with coupled first and second order differences for manifold-valued image processing}, abstract = { We generalize discrete variational models involving the infimal convolution (IC) of first and second order differences and the total generalized variation (TGV) to manifold-valued images. We propose both extrinsic and intrinsic approaches. The extrinsic models are based on embedding the manifold into an Euclidean space of higher dimension with manifold constraints. An alternating direction methods of multipliers can be employed for finding the minimizers. However, the components within the extrinsic IC or TGV decompositions live in the embedding space which makes their interpretation difficult. Therefore we investigate two intrinsic approaches: for Lie groups, we employ the group action within the models; for more general manifolds our IC model is based on recently developed absolute second order differences on manifolds, while our TGV approach uses an approximation of the parallel transport by the pole ladder. For computing the minimizers of the intrinsic models we apply gradient descent algorithms. Numerical examples demonstrate that our approaches work well for certain manifolds. }, } -
Bergmann, R., Fitschen, J. H., Persch, J., Steidl, G.2017Iterative multiplicative filters for data labeling
International Journal of Computer Vision1233435–453Based on an idea of Åström et. al. [2017, JMIV] we propose a new iterative multiplicative filtering algorithm for label assignment matrices which can be used for the supervised partitioning of data. Starting with a row-normalized matrix containing the averaged distances between prior features and observed ones, the method assigns in a very efficient way labels to the data. We interpret the algorithm as a gradient ascent method with respect to a certain function on the product manifold of positive numbers followed by a reprojection onto a subset of the probability simplex consisting of vectors whose components are bounded away from zero by a small constant. While such boundedness away from zero is necessary to avoid an arithmetic underflow, our convergence results imply that they are also necessary for theoretical reasons. Numerical examples show that the proposed simple and fast algorithm leads to very good results. In particular we apply the method for the partitioning of manifold-valued images.
@article{BergmannFitschenPerschSteidl-2017-1, issue = {3}, pages = {435–453}, doi = {10.1007/s11263-017-0995-9}, author = {Bergmann, R. and Fitschen, J. H. and Persch, J. and Steidl, G.}, eprint = {1604.08714}, year = {2017}, eprinttype = {arXiv}, volume = {123}, journaltitle = {International Journal of Computer Vision}, title = {Iterative multiplicative filters for data labeling}, abstract = { Based on an idea of Åström et. al. [2017, JMIV] we propose a new iterative multiplicative filtering algorithm for label assignment matrices which can be used for the supervised partitioning of data. Starting with a row-normalized matrix containing the averaged distances between prior features and observed ones, the method assigns in a very efficient way labels to the data. We interpret the algorithm as a gradient ascent method with respect to a certain function on the product manifold of positive numbers followed by a reprojection onto a subset of the probability simplex consisting of vectors whose components are bounded away from zero by a small constant. While such boundedness away from zero is necessary to avoid an arithmetic underflow, our convergence results imply that they are also necessary for theoretical reasons. Numerical examples show that the proposed simple and fast algorithm leads to very good results. In particular we apply the method for the partitioning of manifold-valued images. }, } -
Bergmann, R., Persch, J., Steidl, G.2016A parallel Douglas–Rachford algorithm for minimizing ROF-like functionals on images with values in symmetric Hadamard manifolds
SIAM Journal on Imaging Sciences93901–937We are interested in restoring images having values in a symmetric Hadamard manifold by minimizing a functional with a quadratic data term and a total variation like regularizing term. To solve the convex minimization problem, we extend the Douglas-Rachford algorithm and its parallel version to symmetric Hadamard manifolds. The core of the Douglas-Rachford algorithm are reflections of the functions involved in the functional to be minimized. In the Euclidean setting the reflections of convex lower semicontinuous functions are nonexpansive. As a consequence, convergence results for Krasnoselski-Mann iterations imply the convergence of the Douglas-Rachford algorithm. Unfortunately, this general results does not carry over to Hadamard manifolds, where proper convex lower semicontinuous functions can have expansive reflections. However, splitting our restoration functional in an appropriate way, we have only to deal with special functions namely, several distance-like functions and an indicator functions of a special convex sets. We prove that the reflections of certain distance-like functions on Hadamard manifolds are nonexpansive which is an interesting result on its own. Furthermore, the reflection of the involved indicator function is nonexpansive on Hadamard manifolds with constant curvature so that the Douglas-Rachford algorithm converges here.
Several numerical examples demonstrate the advantageous performance of the suggested algorithm compared to other existing methods as the cyclic proximal point algorithm or half-quadratic minimization. Numerical convergence is also observed in our experiments on the Hadamard manifold of symmetric positive definite matrices with the affine invariant metric which does not have a constant curvature.
@article{BergmannPerschSteidl-2016, number = {3}, pages = {901–937}, doi = {10.1137/15M1052858}, author = {Bergmann, R. and Persch, J. and Steidl, G.}, eprint = {1512.02814}, year = {2016}, eprinttype = {arXiv}, volume = {9}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {A parallel {D}ouglas–{R}achford algorithm for minimizing {ROF}-like functionals on images with values in symmetric {H}adamard manifolds}, abstract = { We are interested in restoring images having values in a symmetric Hadamard manifold by minimizing a functional with a quadratic data term and a total variation like regularizing term. To solve the convex minimization problem, we extend the Douglas-Rachford algorithm and its parallel version to symmetric Hadamard manifolds. The core of the Douglas-Rachford algorithm are reflections of the functions involved in the functional to be minimized. In the Euclidean setting the reflections of convex lower semicontinuous functions are nonexpansive. As a consequence, convergence results for Krasnoselski-Mann iterations imply the convergence of the Douglas-Rachford algorithm. Unfortunately, this general results does not carry over to Hadamard manifolds, where proper convex lower semicontinuous functions can have expansive reflections. However, splitting our restoration functional in an appropriate way, we have only to deal with special functions namely, several distance-like functions and an indicator functions of a special convex sets. We prove that the reflections of certain distance-like functions on Hadamard manifolds are nonexpansive which is an interesting result on its own. Furthermore, the reflection of the involved indicator function is nonexpansive on Hadamard manifolds with constant curvature so that the Douglas-Rachford algorithm converges here. Several numerical examples demonstrate the advantageous performance of the suggested algorithm compared to other existing methods as the cyclic proximal point algorithm or half-quadratic minimization. Numerical convergence is also observed in our experiments on the Hadamard manifold of symmetric positive definite matrices with the affine invariant metric which does not have a constant curvature. }, } -
Bačák, M., Bergmann, R., Steidl, G., Weinmann, A.2016A second order non-smooth variational model for restoring manifold-valued images
SIAM Journal on Scientific Computing381A567–A597We introduce a new non-smooth variational model for the restoration of manifold-valued data which includes second order differences in the regularization term. While such models were successfully applied for real-valued images, we introduce the second order difference and the corresponding variational models for manifold data, which up to now only existed for cyclic data. The approach requires a combination of techniques from numerical analysis, convex optimization and differential geometry. First, we establish a suitable definition of absolute second order differences for signals and images with values in a manifold. Employing this definition, we introduce a variational denoising model based on first and second order differences in the manifold setup. In order to minimize the corresponding functional, we develop an algorithm using an inexact cyclic proximal point algorithm. We propose an efficient strategy for the computation of the corresponding proximal mappings in symmetric spaces utilizing the machinery of Jacobi fields. For the -sphere and the manifold of symmetric positive definite matrices, we demonstrate the performance of our algorithm in practice. We prove the convergence of the proposed exact and inexact variant of the cyclic proximal point algorithm in Hadamard spaces. These results which are of interest on its own include, e.g., the manifold of symmetric positive definite matrices.
@article{BacakBergmannSteidlWeinmann-2016, number = {1}, pages = {A567–A597}, doi = {10.1137/15M101988X}, author = {Bačák, M. and Bergmann, R. and Steidl, G. and Weinmann, A.}, eprint = {1506.02409}, year = {2016}, eprinttype = {arXiv}, volume = {38}, journaltitle = {SIAM Journal on Scientific Computing}, title = {A second order non-smooth variational model for restoring manifold-valued images}, abstract = { We introduce a new non-smooth variational model for the restoration of manifold-valued data which includes second order differences in the regularization term. While such models were successfully applied for real-valued images, we introduce the second order difference and the corresponding variational models for manifold data, which up to now only existed for cyclic data. The approach requires a combination of techniques from numerical analysis, convex optimization and differential geometry. First, we establish a suitable definition of absolute second order differences for signals and images with values in a manifold. Employing this definition, we introduce a variational denoising model based on first and second order differences in the manifold setup. In order to minimize the corresponding functional, we develop an algorithm using an inexact cyclic proximal point algorithm. We propose an efficient strategy for the computation of the corresponding proximal mappings in symmetric spaces utilizing the machinery of Jacobi fields. For the $n$-sphere and the manifold of symmetric positive definite matrices, we demonstrate the performance of our algorithm in practice. We prove the convergence of the proposed exact and inexact variant of the cyclic proximal point algorithm in Hadamard spaces. These results which are of interest on its own include, e.g., the manifold of symmetric positive definite matrices. }, } -
Bergmann, R., Weinmann, A.2016A second order TV-type approach for inpainting and denoising higher dimensional combined cyclic and vector space data
Journal of Mathematical Imaging and Vision553401–427In this paper we consider denoising and inpainting problems for higher dimensional combined cyclic and linear space valued data. These kind of data appear when dealing with nonlinear color spaces such as HSV, and they can be obtained by changing the space domain of, e.g., an optical flow field to polar coordinates. For such nonlinear data spaces, we develop algorithms for the solution of the corresponding second order total variation (TV) type problems for denoising, inpainting as well as the combination of both. We provide a convergence analysis and we apply the algorithms to concrete problems.
@article{BergmannWeinmann-2016, number = {3}, pages = {401–427}, doi = {10.1007/s10851-015-0627-3}, author = {Bergmann, R. and Weinmann, A.}, eprint = {1501.02684}, year = {2016}, eprinttype = {arXiv}, volume = {55}, journaltitle = {Journal of Mathematical Imaging and Vision}, title = {A second order {TV}-type approach for inpainting and denoising higher dimensional combined cyclic and vector space data}, abstract = { In this paper we consider denoising and inpainting problems for higher dimensional combined cyclic and linear space valued data. These kind of data appear when dealing with nonlinear color spaces such as HSV, and they can be obtained by changing the space domain of, e.g., an optical flow field to polar coordinates. For such nonlinear data spaces, we develop algorithms for the solution of the corresponding second order total variation (TV) type problems for denoising, inpainting as well as the combination of both. We provide a convergence analysis and we apply the algorithms to concrete problems. }, } -
Bergmann, R., Chan, R. H., Hielscher, R., Persch, J., Steidl, G.2016Restoration of manifold-valued images by half-quadratic minimization
Inverse Problems and Imaging102281–304The paper addresses the generalization of the half-quadratic minimization method for the restoration of images having values in a complete, connected Riemannian manifold.
We recall the half-quadratic minimization method using the notation of the -transform and adapt the algorithm to our special variational setting.
We prove the convergence of the method for Hadamard spaces.
Extensive numerical examples for images with values on spheres, in the rotation group , and in the manifold of positive definite matrices demonstrate the excellent performance of the algorithm.
In particular, the method with -valued data shows promising results for the restoration of images obtained from Electron Backscattered Diffraction which are of interest in material science.
@article{BergmannChanHielscherPerschSteidl-2016, number = {2}, pages = {281–304}, doi = {10.3934/ipi.2016001}, author = {Bergmann, R. and Chan, R. H. and Hielscher, R. and Persch, J. and Steidl, G.}, eprint = {1505.07029}, year = {2016}, eprinttype = {arXiv}, volume = {10}, journaltitle = {Inverse Problems and Imaging}, title = {Restoration of manifold-valued images by half-quadratic minimization}, abstract = { The paper addresses the generalization of the half-quadratic minimization method for the restoration of images having values in a complete, connected Riemannian manifold. We recall the half-quadratic minimization method using the notation of the $c$-transform and adapt the algorithm to our special variational setting. We prove the convergence of the method for Hadamard spaces. Extensive numerical examples for images with values on spheres, in the rotation group $\operatorname\{SO\}(3)$, and in the manifold of positive definite matrices demonstrate the excellent performance of the algorithm. In particular, the method with $\operatorname\{SO\}(3)$-valued data shows promising results for the restoration of images obtained from Electron Backscattered Diffraction which are of interest in material science. }, } -
Bergmann, R., Prestin, J.2015Multivariate periodic wavelets of de la Vallée Poussin type
Journal of Fourier Analysis and Applications212342–369In this paper we present a general approach to multivariate periodic wavelets generated by scaling functions of de la Vallée Poussin type. These scaling functions and their corresponding wavelets are determined by their Fourier coefficients, which are sample values of a function, that can be chosen arbitrarily smooth, even with different smoothness in each direction. This construction generalizes the one-dimensional de la Vallée Poussin means to the multivariate case and enables the construction of wavelet systems, where the set of dilation matrices for the two-scale relation of two spaces of the multiresolution analysis may contain shear and rotation matrices. It further enables the functions contained in each of the function spaces from the corresponding series of scaling spaces to have a certain direction or set of directions as their focus, which is illustrated by detecting jumps of certain directional derivatives of higher order.
@article{BergmannPrestin-2015, number = {2}, pages = {342–369}, doi = {10.1007/s00041-014-9372-z}, author = {Bergmann, R. and Prestin, J.}, eprint = {1402.371}, year = {2015}, eprinttype = {arXiv}, volume = {21}, journaltitle = {Journal of Fourier Analysis and Applications}, title = {Multivariate periodic wavelets of de la Vallée Poussin type}, abstract = { In this paper we present a general approach to multivariate periodic wavelets generated by scaling functions of de la Vallée Poussin type. These scaling functions and their corresponding wavelets are determined by their Fourier coefficients, which are sample values of a function, that can be chosen arbitrarily smooth, even with different smoothness in each direction. This construction generalizes the one-dimensional de la Vallée Poussin means to the multivariate case and enables the construction of wavelet systems, where the set of dilation matrices for the two-scale relation of two spaces of the multiresolution analysis may contain shear and rotation matrices. It further enables the functions contained in each of the function spaces from the corresponding series of scaling spaces to have a certain direction or set of directions as their focus, which is illustrated by detecting jumps of certain directional derivatives of higher order. }, } -
Bergmann, R., Laus, F., Steidl, G., Weinmann, A.2014Second order differences of cyclic data and applications in variational denoising
SIAM Journal on Imaging Sciences742916–2953In many image and signal processing applications, such as interferometric synthetic aperture radar (SAR), electroencephalogram (EEG) data analysis, ground-based astronomy, and color image restoration, in HSV or LCh spaces the data has its range on the one-dimensional sphere . Although the minimization of total variation (TV) regularized functionals is among the most popular methods for edge-preserving image restoration, such methods were only very recently applied to cyclic structures. However, as for Euclidean data, TV regularized variational methods suffer from the so-called staircasing effect. This effect can be avoided by involving higher order derivatives into the functional. This is the first paper which uses higher order differences of cyclic data in regularization terms of energy functionals for image restoration. We introduce absolute higher order differences for -valued data in a sound way which is independent of the chosen representation system on the circle. Our absolute cyclic first order difference is just the geodesic distance between points. Similar to the geodesic distances, the absolute cyclic second order differences have only values in . We update the cyclic variational TV approach by our new cyclic second order differences. To minimize the corresponding functional we apply a cyclic proximal point method which was recently successfully proposed for Hadamard manifolds. Choosing appropriate cycles this algorithm can be implemented in an efficient way. The main steps require the evaluation of proximal mappings of our cyclic differences for which we provide analytical expressions. Under certain conditions we prove the convergence of our algorithm. Various numerical examples with artificial as well as real-world data demonstrate the advantageous performance of our algorithm.
@article{BergmannLausSteidlWeinmann-2014, number = {4}, pages = {2916–2953}, doi = {10.1137/140969993}, author = {Bergmann, R. and Laus, F. and Steidl, G. and Weinmann, A.}, eprint = {1405.5349}, year = {2014}, eprinttype = {arXiv}, volume = {7}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {Second order differences of cyclic data and applications in variational denoising}, abstract = { In many image and signal processing applications, such as interferometric synthetic aperture radar (SAR), electroencephalogram (EEG) data analysis, ground-based astronomy, and color image restoration, in HSV or LCh spaces the data has its range on the one-dimensional sphere $\mathbb S^1$. Although the minimization of total variation (TV) regularized functionals is among the most popular methods for edge-preserving image restoration, such methods were only very recently applied to cyclic structures. However, as for Euclidean data, TV regularized variational methods suffer from the so-called staircasing effect. This effect can be avoided by involving higher order derivatives into the functional. This is the first paper which uses higher order differences of cyclic data in regularization terms of energy functionals for image restoration. We introduce absolute higher order differences for $\mathbb S^1$-valued data in a sound way which is independent of the chosen representation system on the circle. Our absolute cyclic first order difference is just the geodesic distance between points. Similar to the geodesic distances, the absolute cyclic second order differences have only values in $[0,\pi]$. We update the cyclic variational TV approach by our new cyclic second order differences. To minimize the corresponding functional we apply a cyclic proximal point method which was recently successfully proposed for Hadamard manifolds. Choosing appropriate cycles this algorithm can be implemented in an efficient way. The main steps require the evaluation of proximal mappings of our cyclic differences for which we provide analytical expressions. Under certain conditions we prove the convergence of our algorithm. Various numerical examples with artificial as well as real-world data demonstrate the advantageous performance of our algorithm. }, } -
Bergmann, R.2013The fast Fourier transform and fast wavelet transform for patterns on the torus
Applied and Computational Harmonic Analysis35139–51We introduce a fast Fourier transform on regular d-dimensional lattices. We investigate properties of congruence class representants, i.e. their ordering, to classify directions and derive a Cooley–Tukey algorithm. Despite the fast Fourier techniques itself, there is also the advantage of this transform to be parallelized efficiently, yielding faster versions than the one-dimensional Fourier transform. These properties of the lattice can further be used to perform a fast multivariate wavelet decomposition, where the wavelets are given as trigonometric polynomials. Furthermore the preferred directions of the decomposition itself can be characterized.
@article{Bergmann-2013-2, number = {1}, pages = {39–51}, doi = {10.1016/j.acha.2012.07.007}, author = {Bergmann, R.}, eprint = {1107.5415v2}, year = {2013}, eprinttype = {arXiv}, volume = {35}, journaltitle = {Applied and Computational Harmonic Analysis}, title = {The fast {F}ourier transform and fast wavelet transform for patterns on the torus}, abstract = { We introduce a fast Fourier transform on regular d-dimensional lattices. We investigate properties of congruence class representants, i.e. their ordering, to classify directions and derive a Cooley–Tukey algorithm. Despite the fast Fourier techniques itself, there is also the advantage of this transform to be parallelized efficiently, yielding faster versions than the one-dimensional Fourier transform. These properties of the lattice can further be used to perform a fast multivariate wavelet decomposition, where the wavelets are given as trigonometric polynomials. Furthermore the preferred directions of the decomposition itself can be characterized. }, }
Book Chapter
-
Bergmann, R., Laus, F., Persch, J., Steidl, G.2019Recent advances in denoising of manifold-valued images
in: Kimmel, R., Tai, X.-C.: Processing, Analyzing and Learning of Images, Shapes, and Forms: Part 2, Chapter 14, Handbook of Numerical Analysis20553–578, Elsevier@incollection{BergmannLausPerschSteidl2019, publisher = {Elsevier}, chapter = {14}, pages = {553–578}, doi = {10.1016/bs.hna.2019.07.005}, booktitle = {Processing, Analyzing and Learning of Images, Shapes, and Forms: Part 2}, author = {Bergmann, R. and Laus, F. and Persch, J. and Steidl, G.}, editor = {Kimmel, R. and Tai, X.-C.}, series = {Handbook of Numerical Analysis}, year = {2019}, volume = {20}, title = {Recent advances in denoising of manifold-valued images}, }
Peer-reviewed Conference Proceedings
-
Bergmann, R., Baran, M.2026Groups and smooth geometry using LieGroups.jl
in: Proceedings of the JuliaCon Conferences879195, The Open JournalLieGroups.jl is a Julia package that provides an interface to define Lie groups as well as the corresponding Lie algebra and Lie group actions. The package also offers a well-documented, performant, and well-tested library of such objects, with a focus on numerical computations in engineering. This paper presents the main features of the interfaces and how that is integrated within the JuliaManifolds ecosystem. We further present an overview on existing Lie groups implemented in LieGroups.jl as well as how to get started to use the package in practice.
@inproceedings{BergmannBaran-2026, publisher = {The Open Journal}, pdf = {https://juliacon.github.io/proceedings-papers/jcon.00195/10.21105.jcon.00195.pdf}, number = {79}, pages = {195}, doi = {10.21105/jcon.00195}, booktitle = {Proceedings of the JuliaCon Conferences}, author = {Bergmann, R. and Baran, M.}, year = {2026}, volume = {8}, title = {Groups and smooth geometry using LieGroups.jl}, abstract = { [LieGroups.jl](https://juliamanifolds.github.io/LieGroups.jl/stable/) is a Julia package that provides an interface to define Lie groups as well as the corresponding Lie algebra and Lie group actions. The package also offers a well-documented, performant, and well-tested library of such objects, with a focus on numerical computations in engineering. This paper presents the main features of the interfaces and how that is integrated within the [JuliaManifolds](https://github.com/JuliaManifolds) ecosystem. We further present an overview on existing Lie groups implemented in LieGroups.jl as well as how to get started to use the package in practice. }, } -
Stokke, J. A., Bergmann, R., Hanik, M., Tychowicz, C. von2026p-Laplacians for Manifold-valued Hypergraphs
in: Nielsen, F., Barbaresco, F.: Geometric Science of Information, GSI 2025162–171 arxiv 2507.10335Hypergraphs extend traditional graphs by enabling the representation of N-ary relationships through higher-order edges. Akin to a common approach of deriving graph Laplacians, we define function spaces and corresponding symmetric products on the nodes and edges to derive hypergraph Laplacians. While this has been done before for Euclidean features, this work generalizes previous hypergraph Laplacian approaches to accommodate manifold-valued hypergraphs for many commonly encountered manifolds.
@inproceedings{StokkeBergmannHanikvonTycowicz-2025, pages = {162–171}, doi = {10.1007/978-3-032-03924-8_17}, booktitle = {Geometric Science of Information, GSI 2025}, author = {Stokke, J. A. and Bergmann, R. and Hanik, M. and Tychowicz, C. von}, editor = {Nielsen, F. and Barbaresco, F.}, eprint = {2507.10335}, year = {2026}, eprinttype = {arxiv}, title = {p-Laplacians for Manifold-valued Hypergraphs}, abstract = { Hypergraphs extend traditional graphs by enabling the representation of N-ary relationships through higher-order edges. Akin to a common approach of deriving graph Laplacians, we define function spaces and corresponding symmetric products on the nodes and edges to derive hypergraph Laplacians. While this has been done before for Euclidean features, this work generalizes previous hypergraph Laplacian approaches to accommodate manifold-valued hypergraphs for many commonly encountered manifolds. }, } -
Bergmann, R., Herrmann, M., Herzog, R., Schmidt, S., Vidal-Núñez, J.2019Geometry processing problems using the total variation of the normal vector field
in: Gesellschaft für Angewandte Mathematik und Mechanik (GAMM): 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), Wiley-BlackwellThis paper presents a novel approach to the formulation and solution of discrete geometry processing problems including mesh denoising. The main quantity of interest is the piecewise constant unit normal vector field, which we consider on piecewise flat, triangulated surfaces. In a similar fashion as one does for images defined on 'flat' domains, our goal is to remove noise while preserving shape features such as sharp edges. To this end, we model a denoising problem via a quadratic vertex tracking term and a regularizer based on the total variation of the normal vector field. Since the latter has values on the unit sphere, its total variation reduces to a finite sum of the geodesic distances of neighboring normals. We solve the model numerically by applying split-Bregmann iterations and provide results for the 'fandisk' benchmark.
@inproceedings{BergmannHerrmannHerzogSchmidtVidal-Nunez-2019, booktitle = {90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM)}, publisher = {Wiley-Blackwell}, author = {Bergmann, R. and Herrmann, M. and Herzog, R. and Schmidt, S. and Vidal-Núñez, J.}, doi = {10.1002/pamm.201900189}, year = {2019}, title = {Geometry processing problems using the total variation of the normal vector field}, abstract = { This paper presents a novel approach to the formulation and solution of discrete geometry processing problems including mesh denoising. The main quantity of interest is the piecewise constant unit normal vector field, which we consider on piecewise flat, triangulated surfaces. In a similar fashion as one does for images defined on 'flat' domains, our goal is to remove noise while preserving shape features such as sharp edges. To this end, we model a denoising problem via a quadratic vertex tracking term and a regularizer based on the total variation of the normal vector field. Since the latter has values on the unit sphere, its total variation reduces to a finite sum of the geodesic distances of neighboring normals. We solve the model numerically by applying split-Bregmann iterations and provide results for the 'fandisk' benchmark. }, editor = {Gesellschaft für Angewandte Mathematik und Mechanik (GAMM)}, } -
Bergmann, R., Herzog, R., Loayza-Romero, E., Welker, K.2019Shape optimization: what to do first, optimize or discretize?
in: Gesellschaft für Angewandte Mathematik und Mechanik (GAMM): 90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM), Wiley-BlackwellIn general, it is not easy to decide whether to use a discretize–then–optimize or optimize–then–discretize approach to solve PDE-constrained optimization problems. Shape optimization problems are particularly challenging due to the infinite dimensional, nonlinear structure of shape spaces. One option to overcome this drawback is to choose finite dimensional shape spaces, i.e., to discretize first. Nevertheless, this limits the amount of available tools coming from function spaces. In this note, we aim to show advantages and disadvantages of both approaches based on a simple shape optimization problem.
@inproceedings{BergmannHerzogLoayzaWelker2019, booktitle = {90th Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM)}, publisher = {Wiley-Blackwell}, author = {Bergmann, R. and Herzog, R. and Loayza-Romero, E. and Welker, K.}, year = {2019}, doi = {10.1002/pamm.201900067}, title = {Shape optimization: what to do first, optimize or discretize?}, abstract = { In general, it is not easy to decide whether to use a discretize–then–optimize or optimize–then–discretize approach to solve PDE-constrained optimization problems. Shape optimization problems are particularly challenging due to the infinite dimensional, nonlinear structure of shape spaces. One option to overcome this drawback is to choose finite dimensional shape spaces, i.e., to discretize first. Nevertheless, this limits the amount of available tools coming from function spaces. In this note, we aim to show advantages and disadvantages of both approaches based on a simple shape optimization problem. }, editor = {Gesellschaft für Angewandte Mathematik und Mechanik (GAMM)}, } -
Bergmann, R., Merkert, D.2017Approximation of periodic PDE solutions with anisotropic translation invariant spaces
in: 2017 International Conference on Sampling Theory and Applications (SampTA)396-399We approximate the quasi-static equation of linear elasticity in translation invariant spaces on the torus. This unifies different FFT-based discretisation methods into a common framework and extends them to anisotropic lattices. We analyse the connection between the discrete solution spaces and demonstrate the numerical benefits. Finite element methods arise as a special case of periodised Box spline translates.
@inproceedings{BergmannMerkert-2017, booktitle = {2017 International Conference on Sampling Theory and Applications (SampTA)}, author = {Bergmann, R. and Merkert, D.}, doi = {10.1109/SAMPTA.2017.8024347}, pages = {396-399}, title = {Approximation of periodic PDE solutions with anisotropic translation invariant spaces}, abstract = { We approximate the quasi-static equation of linear elasticity in translation invariant spaces on the torus. This unifies different FFT-based discretisation methods into a common framework and extends them to anisotropic lattices. We analyse the connection between the discrete solution spaces and demonstrate the numerical benefits. Finite element methods arise as a special case of periodised Box spline translates. }, year = {2017}, } -
Bergmann, R., Fitschen, J. H., Persch, J., Steidl, G.2017Infimal Convolution Coupling of First and Second Order Differences on Manifold-Valued Images
in: Lauze, F., Dong, Y., Dahl, A. B.: Scale Space and Variational Methods in Computer Vision: 6th International Conference, SSVM 2017, Kolding, Denmark, June 4-8, 2017, Proceedings447–459, Springer International PublishingRecently infimal convolution type functions were used in regularization terms of variational models for restoring and decomposing images. This is the first attempt to generalize the infimal convolution of first and second order differences to manifold-valued images. We propose both an extrinsic and an intrinsic approach. Our focus is on the second one since the summands arising in the infimal convolution lie on the manifold themselves and not in the higher dimensional embedding space. We demonstrate by numerical examples that the approach works well on the circle, the 2-sphere, the rotation group, and the manifold of positive definite matrices with the affine invariant metric.
@inproceedings{BergmannFitschenPerschSteidl-2017-2, publisher = {Springer International Publishing}, pages = {447–459}, doi = {10.1007/978-3-319-58771-4_36}, booktitle = {Scale Space and Variational Methods in Computer Vision: 6th International Conference, SSVM 2017, Kolding, Denmark, June 4-8, 2017, Proceedings}, author = {Bergmann, R. and Fitschen, J. H. and Persch, J. and Steidl, G.}, editor = {Lauze, F. and Dong, Y. and Dahl, A. B.}, year = {2017}, title = {Infimal Convolution Coupling of First and Second Order Differences on Manifold-Valued Images}, abstract = { Recently infimal convolution type functions were used in regularization terms of variational models for restoring and decomposing images. This is the first attempt to generalize the infimal convolution of first and second order differences to manifold-valued images. We propose both an extrinsic and an intrinsic approach. Our focus is on the second one since the summands arising in the infimal convolution lie on the manifold themselves and not in the higher dimensional embedding space. We demonstrate by numerical examples that the approach works well on the circle, the 2-sphere, the rotation group, and the manifold of positive definite matrices with the affine invariant metric. }, } -
Bergmann, R.2017MVIRT A toolbox for manifold-valued image restoration
in: IEEE International Conference on Image Processing, IEEE ICIP 2017, Beijing, China, September 17–20, 2017In many real life application measured data takes its values on Riemannian manifolds. For the special case of the Euclidean space this setting includes the classical grayscale and color images. Like these classical images, manifold-valued data might suffer from measurement errors in form of noise or missing data. In this paper we present the manifold-valued image restoration toolbox (MVIRT) that provides implementations of classical image processing tasks. Based on recent developments in variational methods for manifold-valued image processing methods, like total variation regularization, the toolbox provides easy access to work with these algorithms. The toolbox is implemented in Matlab, open source, and easily extendible, e.g. with own manifolds, noise models or further algorithms. This paper introduces the main mathematical methods as well as numerical examples.
@inproceedings{Bergmann-2017, booktitle = {IEEE International Conference on Image Processing, IEEE ICIP 2017, Beijing, China, September 17–20, 2017}, author = {Bergmann, R.}, doi = {10.1109/ICIP.2017.8296271}, year = {2017}, title = {MVIRT A toolbox for manifold-valued image restoration}, abstract = { In many real life application measured data takes its values on Riemannian manifolds. For the special case of the Euclidean space this setting includes the classical grayscale and color images. Like these classical images, manifold-valued data might suffer from measurement errors in form of noise or missing data. In this paper we present the manifold-valued image restoration toolbox (MVIRT) that provides implementations of classical image processing tasks. Based on recent developments in variational methods for manifold-valued image processing methods, like total variation regularization, the toolbox provides easy access to work with these algorithms. The toolbox is implemented in Matlab, open source, and easily extendible, e.g. with own manifolds, noise models or further algorithms. This paper introduces the main mathematical methods as well as numerical examples. }, } -
Bergmann, R., Tenbrinck, T.2017Nonlocal inpainting of manifold-valued data on finite weighted graphs
in: Nielsen, F., Barbaresco, F.: Geometric Science of Information – 3rd Conference on Geometric Science of Information604–612, Springer International Publishing arXiv 1704.06424Recently, there has been a strong ambition to translate models and algorithms from traditional image processing to non-Euclidean domains, e.g., to manifold-valued data. While the task of denoising has been extensively studied in the last years, there was rarely an attempt to perform image inpainting on manifold-valued data. In this paper we present a nonlocal inpainting method for manifold-valued data given on a finite weighted graph. We introduce a new graph infinity-Laplace operator based on the idea of discrete minimizing Lipschitz extensions, which we use to formulate the inpainting problem as PDE on the graph. Furthermore, we derive an explicit numerical solving scheme, which we evaluate on two classes of synthetic manifold-valued images.
@inproceedings{BergmannTenbrinck-2017, publisher = {Springer International Publishing}, pages = {604–612}, doi = {10.1007/978-3-319-68445-1}, booktitle = {Geometric Science of Information – 3rd Conference on Geometric Science of Information}, author = {Bergmann, R. and Tenbrinck, T.}, editor = {Nielsen, F. and Barbaresco, F.}, eprint = {1704.06424}, year = {2017}, eprinttype = {arXiv}, title = {Nonlocal inpainting of manifold-valued data on finite weighted graphs}, abstract = { Recently, there has been a strong ambition to translate models and algorithms from traditional image processing to non-Euclidean domains, e.g., to manifold-valued data. While the task of denoising has been extensively studied in the last years, there was rarely an attempt to perform image inpainting on manifold-valued data. In this paper we present a nonlocal inpainting method for manifold-valued data given on a finite weighted graph. We introduce a new graph infinity-Laplace operator based on the idea of discrete minimizing Lipschitz extensions, which we use to formulate the inpainting problem as PDE on the graph. Furthermore, we derive an explicit numerical solving scheme, which we evaluate on two classes of synthetic manifold-valued images. }, } -
Bergmann, R., Weinmann, A.2015Inpainting of cyclic data using first and second order differences
in: Tai, X.-C., Bae, E., Chan, T. F., Leung, S. Y., Lysaker, M.: Energy Minimization Methods in Computer Vision and Pattern Recognition, 10th International Conference on, EMMCVPR 2015, Hong Kong155–168, Springer arXiv 1410.1998Cyclic data arise in various image and signal processing applications such as interferometric synthetic aperture radar, electroencephalogram data analysis, and color image restoration in HSV or LCh spaces. In this paper we introduce a variational inpainting model for cyclic data which utilizes our definition of absolute cyclic second order differences. Based on analytical expressions for the proximal mappings of these differences we propose a cyclic proximal point algorithm (CPPA) for minimizing the corresponding functional. We choose appropriate cycles to implement this algorithm in an efficient way. We further introduce a simple strategy to initialize the unknown inpainting region. Numerical results both for synthetic and real-world data demonstrate the performance of our algorithm.
@inproceedings{BergmannWeinmann-2015, publisher = {Springer}, pages = {155–168}, doi = {10.1007/978-3-319-14612-6_12}, booktitle = {Energy Minimization Methods in Computer Vision and Pattern Recognition, 10th International Conference on, EMMCVPR 2015, Hong Kong}, author = {Bergmann, R. and Weinmann, A.}, editor = {Tai, X.-C. and Bae, E. and Chan, T. F. and Leung, S. Y. and Lysaker, M.}, eprint = {1410.1998}, year = {2015}, eprinttype = {arXiv}, title = {Inpainting of cyclic data using first and second order differences}, abstract = { Cyclic data arise in various image and signal processing applications such as interferometric synthetic aperture radar, electroencephalogram data analysis, and color image restoration in HSV or LCh spaces. In this paper we introduce a variational inpainting model for cyclic data which utilizes our definition of absolute cyclic second order differences. Based on analytical expressions for the proximal mappings of these differences we propose a cyclic proximal point algorithm (CPPA) for minimizing the corresponding functional. We choose appropriate cycles to implement this algorithm in an efficient way. We further introduce a simple strategy to initialize the unknown inpainting region. Numerical results both for synthetic and real-world data demonstrate the performance of our algorithm. }, } -
Oezguen, N., Schubert, K., Bergmann, R., Bennewitz, R., Strauss, D. J.2015Relating tribological stimuli to somatosensory electroencephalographic responses
in: Engineering in Medicine and Biology Society (EMBC), 37th Annual International Conference of the IEEE8115-8118The present study deals with the extraction of neural correlates evoked by tactile stimulation of the human fingertip. A reciprocal sliding procedure was performed using a home-built tribometer while simultaneously electroencephalographic (EEG) data from the somatosensory cortex was recorded. The tactile stimuli were delivered by a sliding block with equidistant, perpendicular ridges. The experiments were designed and performed in a fully passive way to prevent attentional locked influences from the subjects. In order to improve the signal-to-noise ratio (SNR) of event related single-trials (ERPs), nonlocal means in addition to 2D-anisotropic denoising schemes based on tight Gabor frames were applied. This novel approach allowed for an easier extraction of ERP alternations. A negative correlation between the latency of the P100 component of the resulting brain responses and the intensity of the underlying lateral forces was found. These findings lead to the conclusion that an increasing stimulus intensity results in a decreasing latency of the brain responses.
@inproceedings{OezguenSchuberBergmannBennewitzStrauss-2015, booktitle = {Engineering in Medicine and Biology Society (EMBC), 37th Annual International Conference of the IEEE}, author = {Oezguen, N. and Schubert, K. and Bergmann, R. and Bennewitz, R. and Strauss, D. J.}, doi = {10.1109/EMBC.2015.7320277}, pages = {8115-8118}, title = {Relating tribological stimuli to somatosensory electroencephalographic responses}, abstract = { The present study deals with the extraction of neural correlates evoked by tactile stimulation of the human fingertip. A reciprocal sliding procedure was performed using a home-built tribometer while simultaneously electroencephalographic (EEG) data from the somatosensory cortex was recorded. The tactile stimuli were delivered by a sliding block with equidistant, perpendicular ridges. The experiments were designed and performed in a fully passive way to prevent attentional locked influences from the subjects. In order to improve the signal-to-noise ratio (SNR) of event related single-trials (ERPs), nonlocal means in addition to 2D-anisotropic denoising schemes based on tight Gabor frames were applied. This novel approach allowed for an easier extraction of ERP alternations. A negative correlation between the latency of the P100 component of the resulting brain responses and the intensity of the underlying lateral forces was found. These findings lead to the conclusion that an increasing stimulus intensity results in a decreasing latency of the brain responses. }, year = {2015}, } -
Bergmann, R., Prestin, J.2014Multivariate anisotropic interpolation on the torus
in: Fasshauer, G., Schumaker, L.: Approximation Theory XIV: San Antonio 201327–44 arXiv 1309.3432We investigate the error of periodic interpolation, when sampling a function on an arbitrary pattern on the torus. We generalize the periodic Strang-Fix conditions to an anisotropic setting and provide an upper bound for the error of interpolation. These conditions and the investigation of the error especially take different levels of smoothness along certain directions into account.
@inproceedings{BergmannPrestin-2014, pages = {27–44}, doi = {10.1007/978-3-319-06404-8_3}, booktitle = {Approximation Theory XIV: San Antonio 2013}, author = {Bergmann, R. and Prestin, J.}, editor = {Fasshauer, G. and Schumaker, L.}, eprint = {1309.3432}, year = {2014}, eprinttype = {arXiv}, title = {Multivariate anisotropic interpolation on the torus}, abstract = { We investigate the error of periodic interpolation, when sampling a function on an arbitrary pattern on the torus. We generalize the periodic Strang-Fix conditions to an anisotropic setting and provide an upper bound for the error of interpolation. These conditions and the investigation of the error especially take different levels of smoothness along certain directions into account. }, }
-
Bergmann, R.2018Variational Methods for Manifold-valued Image Processing
cumulative habilitation thesis, Technische Universität Kaiserslautern@thesis{Bergmann-2018, author = {Bergmann, R.}, year = {2018}, school = {Technische Universität Kaiserslautern}, title = {Variational Methods for Manifold-valued Image Processing}, type = {cumulative habilitation thesis}, } -
Bergmann, R.2013Translationsinvariante Räume multivariater anisotroper Funktionen auf dem Torus
Dissertation, german, Universität zu Lübeck similarily: Shaker Verlag, ISBN 978-3844022667, 2013Die translationsinvarianten Räume sind seit Ende der 1980er Jahre ein wichtiges Werkzeug in der Zerlegung und Analyse von Daten und Funktionen. Sie stellen eine Funktion in verschiedenen Detailstufen dar, wobei sich auf jeder Stufe lokale Eigenschaften der Funktion in den Koeffizienten der Translate wiederfinden. Dazu ist es notwendig, dass die Funktionen einer solchen Zerlegung gut lokalisiert sind. Dies überträgt sich dann auf die von den Translaten der Wavelets aufgespannten orthogonalen Komplemente innerhalb der gestaffelten Räume. Neben diesen theoretischen Eigenschaften haben vor allem die schnellen Algorithmen der Wavelet-Transformation zur großen Verbreitung und Anwendung der Wavelets geführt. In den 1990er Jahren wurden periodische Wavelets entwickelt und in den letzten Jahren mehrdimensionale Wavelets, wie die Shearlets oder Curvelets, die insbesondere spezielle Richtungen in der Zerlegung einer Funktion bevorzugen.
Diese Arbeit widmet sich den mehrdimensionalen periodischen translationsinvarianten Räumen, die insbesondere allgemeiner sind als diejenigen, die lediglich durch Tensorproduktbildung aus dem Eindimensionalen hervorgehen, und somit eine Anisotropie in ihren Fourier- Koeffizienten besitzen und gewisse Richtungseigenschaften haben. Diese Richtungspräferenz spiegelt sich auch in den Mustern wider, mit denen die Translate der Funktionen die hier betrachteten Räume bilden.
Zunächst wird für die periodischen translationsinvarianten Räume auf dem Torus der Interpolationsfehler betrachtet. Dazu werden die anisotropen periodischen Strang-Fix-Bedingungen eingeführt und mit ihnen Fehlerabschätzungen angegeben, welche die Räume bezüglich der Approximationsgüte für Funktionen mit bestimmten Glattheitseigenschaften charakterisieren.
Für die anisotrope periodische Wavelet-Transformation werden Algorithmen vorgestellt, die in ihrer Komplexität den schnellen Algorithmen der eindimensionalen Wavelets entsprechen und dabei insbesondere dimensionsunabhängig sind. Wichtigste Werkzeuge sind dazu die schnelle Fourier-Transformation und die den Wavelets zu Grunde liegenden Zwei-Skalen-Gleichungen der Multiskalen-Analyse. Außerdem wird durch diese Beschreibung eine Richtungsklassifikation der betrachteten Wavelets auf den Mustern möglich.
Ausgehend von den de la Vallée Poussin-Mitteln wird dann eine Verallgemeinerung vorgestellt, bei der lokalisierte anisotrope periodische Wavelets konstruiert werden, deren Fourier-Koeffizienten als Abtastung einer beliebig glatten Funktion gegeben sind, deren Träger endlich ist. Dies verallgemeinert sowohl die eindimensionalen de la Vallée Poussin-Wavelets als auch die multivariaten Dirichlet-Wavelets. Für spezielle glatte Funktionen gelingt es, in der Konstruktion anstelle der rekursiven Definition eine explizite Darstellung der Fourier-Koeffizienten anzugeben und somit für diese lokalisierten Wavelets eine gesamte Multiskalen-Analyse zu konstruieren.
@thesis{Bergmann-2013-1, pdf = {/theses/Bergmann__Translationsinvariante_Raeume_multivariater_anisotroper_Funktionen_auf_dem_Torus.pdf}, school = {Universität zu Lübeck}, language = {german}, isbn_link = {https://www.shaker.de/de/content/catalogue/index.asp?lang=de&ID=8&ISBN=978-3-8440-2266-7}, author = {Bergmann, R.}, note = {similarily: Shaker Verlag, ISBN 978-3844022667, 2013}, isbn = {978-3-8440-2266-7}, year = {2013}, title = {Translationsinvariante Räume multivariater anisotroper Funktionen auf dem Torus}, abstract = { Die translationsinvarianten Räume sind seit Ende der 1980er Jahre ein wichtiges Werkzeug in der Zerlegung und Analyse von Daten und Funktionen. Sie stellen eine Funktion in verschiedenen Detailstufen dar, wobei sich auf jeder Stufe lokale Eigenschaften der Funktion in den Koeffizienten der Translate wiederfinden. Dazu ist es notwendig, dass die Funktionen einer solchen Zerlegung gut lokalisiert sind. Dies überträgt sich dann auf die von den Translaten der Wavelets aufgespannten orthogonalen Komplemente innerhalb der gestaffelten Räume. Neben diesen theoretischen Eigenschaften haben vor allem die schnellen Algorithmen der Wavelet-Transformation zur großen Verbreitung und Anwendung der Wavelets geführt. In den 1990er Jahren wurden periodische Wavelets entwickelt und in den letzten Jahren mehrdimensionale Wavelets, wie die Shearlets oder Curvelets, die insbesondere spezielle Richtungen in der Zerlegung einer Funktion bevorzugen. Diese Arbeit widmet sich den mehrdimensionalen periodischen translationsinvarianten Räumen, die insbesondere allgemeiner sind als diejenigen, die lediglich durch Tensorproduktbildung aus dem Eindimensionalen hervorgehen, und somit eine Anisotropie in ihren Fourier- Koeffizienten besitzen und gewisse Richtungseigenschaften haben. Diese Richtungspräferenz spiegelt sich auch in den Mustern wider, mit denen die Translate der Funktionen die hier betrachteten Räume bilden. Zunächst wird für die periodischen translationsinvarianten Räume auf dem Torus der Interpolationsfehler betrachtet. Dazu werden die anisotropen periodischen Strang-Fix-Bedingungen eingeführt und mit ihnen Fehlerabschätzungen angegeben, welche die Räume bezüglich der Approximationsgüte für Funktionen mit bestimmten Glattheitseigenschaften charakterisieren. Für die anisotrope periodische Wavelet-Transformation werden Algorithmen vorgestellt, die in ihrer Komplexität den schnellen Algorithmen der eindimensionalen Wavelets entsprechen und dabei insbesondere dimensionsunabhängig sind. Wichtigste Werkzeuge sind dazu die schnelle Fourier-Transformation und die den Wavelets zu Grunde liegenden Zwei-Skalen-Gleichungen der Multiskalen-Analyse. Außerdem wird durch diese Beschreibung eine Richtungsklassifikation der betrachteten Wavelets auf den Mustern möglich. Ausgehend von den de la Vallée Poussin-Mitteln wird dann eine Verallgemeinerung vorgestellt, bei der lokalisierte anisotrope periodische Wavelets konstruiert werden, deren Fourier-Koeffizienten als Abtastung einer beliebig glatten Funktion gegeben sind, deren Träger endlich ist. Dies verallgemeinert sowohl die eindimensionalen de la Vallée Poussin-Wavelets als auch die multivariaten Dirichlet-Wavelets. Für spezielle glatte Funktionen gelingt es, in der Konstruktion anstelle der rekursiven Definition eine explizite Darstellung der Fourier-Koeffizienten anzugeben und somit für diese lokalisierten Wavelets eine gesamte Multiskalen-Analyse zu konstruieren. }, type = {Dissertation}, } -
Bergmann, R.2009Interaktive und automatisierte Hypergraphenvisualisierung mittels NURBS-Kurven
Diplomarbeit, german, Universität zu LübeckFür wissenschaftliche Arbeiten in der Graphentheorie, vor allem bei den allgemeineren Hypergraphen, sind Darstellungen zur Erklärung und Erläuterung von großer Bedeutung. Diese Arbeit schafft daher die Grundlagen einer Darstellung von Hypergraphen, die in dem Programm „Gravel“, einem Editor für ebendiese, umgesetzt wurden.
Für Bilder von Hypergraphen werden in dieser Arbeit theoretische Grundlagen entwickelt, die auf Basis der NURBS-Kurven eine Darstellung der Hyperkanten ermöglicht. Dazu werden die Eigenschaften von periodischen NURBS-Kurven betrachtet und Algorithmen zur interaktiven Modifikation vorgestellt. Der Begriff des Hyperkantenumrisses und seiner Gültigkeit wird eingeführt, um formelle Anforderungen an die Darstellung zu schaffen. Auf Grundlage der genannten Begriffe wird das Programm „Gravel“ zum Zeichnen von Graphen und Hypergraphen entwickelt und implementiert.
@thesis{Bergmann-2009, pdf = {http://ronnybergmann.net/theses/Bergmann__Interaktive_und_automatisierte_Hypergraphenvisualisierung_mittels_NURBS-Kurven.pdf}, school = {Universität zu Lübeck}, language = {german}, author = {Bergmann, R.}, year = {2009}, title = {Interaktive und automatisierte Hypergraphenvisualisierung mittels NURBS-Kurven}, abstract = { Für wissenschaftliche Arbeiten in der Graphentheorie, vor allem bei den allgemeineren Hypergraphen, sind Darstellungen zur Erklärung und Erläuterung von großer Bedeutung. Diese Arbeit schafft daher die Grundlagen einer Darstellung von Hypergraphen, die in dem Programm „Gravel“, einem Editor für ebendiese, umgesetzt wurden. Für Bilder von Hypergraphen werden in dieser Arbeit theoretische Grundlagen entwickelt, die auf Basis der NURBS-Kurven eine Darstellung der Hyperkanten ermöglicht. Dazu werden die Eigenschaften von periodischen NURBS-Kurven betrachtet und Algorithmen zur interaktiven Modifikation vorgestellt. Der Begriff des Hyperkantenumrisses und seiner Gültigkeit wird eingeführt, um formelle Anforderungen an die Darstellung zu schaffen. Auf Grundlage der genannten Begriffe wird das Programm „Gravel“ zum Zeichnen von Graphen und Hypergraphen entwickelt und implementiert. }, type = {Diplomarbeit}, }
Theses
-
Seth D. Axen, Baran, M., Bergmann, R.since 2019Manifolds.jl
, Zenodo@software{manifolds-zenodo-mostrecent, publisher = {Zenodo}, doi = {10.5281/ZENODO.4292129}, author = {Seth D. Axen and Baran, M. and Bergmann, R.}, copyright = {MIT License}, year = {since 2019}, title = {Manifolds.jl}, } -
Bergmann, R.since 2016Manopt.jl
, Zenodo@software{manoptjl-zenodo-mostrecent, publisher = {Zenodo}, doi = {10.5281/zenodo.4290905}, author = {Bergmann, R.}, copyright = {MIT License}, year = {since 2016}, title = {Manopt.jl}, }
Software
-
Christmas, J., Bergmann, R., Zhakatayev, A., Rebenda, J., Sing, S.2022Modelling Fire Incidents Response Times in Ålesund
ECMI Annual Report 202240–49 The arXiv preprint is an extended version of the report@misc{CBZRS23, pages = {40–49}, author = {Christmas, J. and Bergmann, R. and Zhakatayev, A. and Rebenda, J. and Sing, S.}, publication date = {01-12-2022}, eprint = {2409.15282}, note = {The arXiv preprint is an extended version of the report}, year = {2022}, eprinttype = {arXiv}, journaltitle = {ECMI Annual Report 2022}, title = {Modelling Fire Incidents Response Times in Ålesund}, } -
Bergmann, R., Laus, F., Persch, J., Steidl, G.2017Manifold-valued Image Processing
Siam News5081 & 3@misc{BergmannLausPerschSteidl-2017, number = {8}, pages = {1 & 3}, author = {Bergmann, R. and Laus, F. and Persch, J. and Steidl, G.}, year = {2017}, volume = {50}, journaltitle = {Siam News}, title = {Manifold-valued Image Processing}, }
Misc
This work by Ronny Bergmann
is licensed under
CC BY-NC-SA 4.0.
Last modified: February 18, 2026.
Website built with Franklin.jl and the Julia programming language.