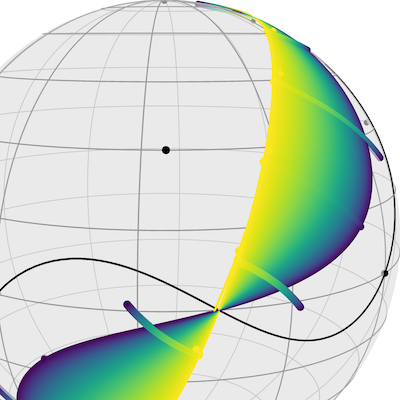
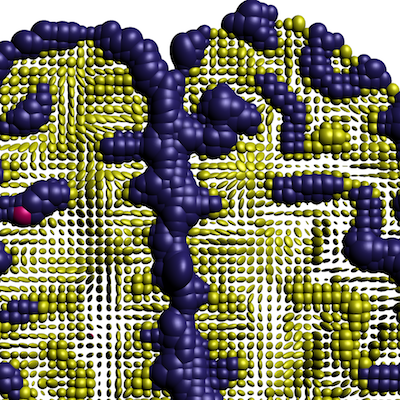
In this paper, we consider the variational regularization of manifold-valued data in the inverse problems setting. In particular, we consider total variation and total generalized variation regularization for manifold-valued data with indirect measurement operators. We provide results on the well-posedness and present algorithms for a numerical realization of these models in the manifold setup. Further, we provide experimental results for synthetic and real data to show the potential of the proposed schemes for applications.
Non-Smooth Variational Models with Second Order and Local Anisotropy Priors for Restoring Cyclic and Manifold-Valued Images
Variational methods in imaging are nowadays developing towards a quite universal and flexible tool, allowing for highly successful approaches on various imaging tasks. Many useful techniques rely on non-smooth, convex functionals. Combinations of first and second order derivatives in regularization functionals or the incorporation of anisotropies steered by the local structures of the image have led to very powerful image restoration techniques. Splitting algorithms together with primal-dual optimization methods are the state-of-the-art techniques for minimizing these functionals. Their strength consists in the splitting of the original problem into a sequence of proximal mappings which can be computed efficiently.
In various applications in image processing and computer vision the functions of interest take values on the circle or in manifolds. Although manifolds play an important role in these fields for a long time, there are only few papers which combine results on non-smooth optimization which were recently extensively exploited in real-valued image processing with manifold-valued settings. This leaves high potential for future research.
In our project we want to generalize convex models for the restoration of real-valued images to cyclic and manifold-valued images. We want to focus on symmetric spaces having applications in image processing. For Hadamard spaces the models are still convex which is in general, e.g., for spheres, not the case. A specific feature of our models is that their regularization terms will incorporate first and second order differences or directional anisotropies. The challenges of our project include the appropriate construction of restoration models for manifold-valued signals and images, the analysis of the models, and the development of efficient minimization algorithms, including convergence results. There is a rich potential for applications of the methods which will be developed within our project. Among others we will use our models for the analysis of Electroencephalographical data and of Electron Backscattered Diffraction data. A publicly available software package is planed as well.
References
- StorathWeinmann-2020
Storath, M., Weinmann, A.2020Variational Regularization of Inverse Problems for Manifold-Valued Data
Information and Inference: A Journal of the IMA@article{StorathWeinmann-2020, eprint = {1804.10432}, author = {Storath, M. and Weinmann, A.}, month = {6}, journaltitle = {Information and Inference: A Journal of the IMA}, year = {2020}, doi = {10.1093/imaiai/iaaa010}, eprinttype = {arXiv}, title = {Variational Regularization of Inverse Problems for Manifold-Valued Data}, abstract = { In this paper, we consider the variational regularization of manifold-valued data in the inverse problems setting. In particular, we consider total variation and total generalized variation regularization for manifold-valued data with indirect measurement operators. We provide results on the well-posedness and present algorithms for a numerical realization of these models in the manifold setup. Further, we provide experimental results for synthetic and real data to show the potential of the proposed schemes for applications. }, } - EHGDSNBW-2019
Esposito, M., Hennersperger, C., Gobl, R., Demaret, L., Storath, M., Navab, M., Baust, M., Weinmann, A.2019Total Variation Regularization of Pose Signals With an Application to 3D Freehand Ultrasound
IEEE Transactions on Medical Imaging38102245–2258@article{EHGDSNBW-2019, volume = {38}, author = {Esposito, M. and Hennersperger, C. and Gobl, R. and Demaret, L. and Storath, M. and Navab, M. and Baust, M. and Weinmann, A.}, number = {10}, year = {2019}, pages = {2245–2258}, doi = {10.1109/tmi.2019.2898480}, journaltitle = {IEEE Transactions on Medical Imaging}, title = {Total Variation Regularization of Pose Signals With an Application to 3D Freehand Ultrasound}, } - BrediesHollerStorathWeinmann:2018-1
Bredies, K., Holler, H., Storath, M., Weinmann, A.2018Total Generalized Variation for Manifold-Valued Data
{SIAM} Journal on Imaging Sciences1131785–1848@article{BrediesHollerStorathWeinmann:2018-1, number = {3}, author = {Bredies, K. and Holler, H. and Storath, M. and Weinmann, A.}, volume = {11}, journaltitle = {{SIAM} Journal on Imaging Sciences}, pages = {1785–1848}, doi = {10.1137/17M1147597}, year = {2018}, title = {Total Generalized Variation for Manifold-Valued Data}, } - BergmannGousenburger-2018
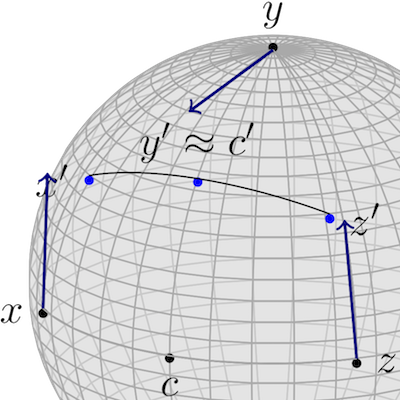
Bergmann, R., Gousenbourger, P.-Y.2018A variational model for data fitting on manifolds by minimizing the acceleration of a Bézier curve
Frontiers in Applied Mathematics and StatisticsWe derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem.
@article{BergmannGousenburger-2018, doi = {10.3389/fams.2018.00059}, author = {Bergmann, R. and Gousenbourger, P.-Y.}, eprint = {1807.10090}, year = {2018}, eprinttype = {arXiv}, journaltitle = {Frontiers in Applied Mathematics and Statistics}, title = {A variational model for data fitting on manifolds by minimizing the acceleration of a {B}ézier curve}, abstract = { We derive a variational model to fit a composite Bézier curve to a set of data points on a Riemannian manifold. The resulting curve is obtained in such a way that its mean squared acceleration is minimal in addition to remaining close the data points. We approximate the acceleration by discretizing the squared second order derivative along the curve. We derive a closed-form, numerically stable and efficient algorithm to compute the gradient of a Bézier curve on manifolds with respect to its control points, expressed as a concatenation of so-called adjoint Jacobi fields. Several examples illustrate the capabilities and validity of this approach both for interpolation and approximation. The examples also illustrate that the approach outperforms previous works tackling this problem. }, } - LausNikolovaPerschSteidl-2017
Laus, F., Mila Nikolova, Persch, J., Steidl, G.2017A Nonlocal Denoising Algorithm for Manifold-Valued Images Using Second Order Statistics
SIAM Journal on Imaging Sciences101416–448@article{LausNikolovaPerschSteidl-2017, number = {1}, author = {Laus, F. and Mila Nikolova and Persch, J. and Steidl, G.}, volume = {10}, year = {2017}, pages = {416–448}, doi = {10.1137/16m1087114}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {A Nonlocal Denoising Algorithm for Manifold-Valued Images Using Second Order Statistics}, } - BergmannFitschenPerschSteidl-2017-1
Bergmann, R., Fitschen, J. H., Persch, J., Steidl, G.2017Iterative multiplicative filters for data labeling
International Journal of Computer Vision1233435–453Based on an idea of Åström et. al. [2017, JMIV] we propose a new iterative multiplicative filtering algorithm for label assignment matrices which can be used for the supervised partitioning of data. Starting with a row-normalized matrix containing the averaged distances between prior features and observed ones, the method assigns in a very efficient way labels to the data. We interpret the algorithm as a gradient ascent method with respect to a certain function on the product manifold of positive numbers followed by a reprojection onto a subset of the probability simplex consisting of vectors whose components are bounded away from zero by a small constant. While such boundedness away from zero is necessary to avoid an arithmetic underflow, our convergence results imply that they are also necessary for theoretical reasons. Numerical examples show that the proposed simple and fast algorithm leads to very good results. In particular we apply the method for the partitioning of manifold-valued images.
@article{BergmannFitschenPerschSteidl-2017-1, issue = {3}, pages = {435–453}, doi = {10.1007/s11263-017-0995-9}, author = {Bergmann, R. and Fitschen, J. H. and Persch, J. and Steidl, G.}, eprint = {1604.08714}, year = {2017}, eprinttype = {arXiv}, volume = {123}, journaltitle = {International Journal of Computer Vision}, title = {Iterative multiplicative filters for data labeling}, abstract = { Based on an idea of Åström et. al. [2017, JMIV] we propose a new iterative multiplicative filtering algorithm for label assignment matrices which can be used for the supervised partitioning of data. Starting with a row-normalized matrix containing the averaged distances between prior features and observed ones, the method assigns in a very efficient way labels to the data. We interpret the algorithm as a gradient ascent method with respect to a certain function on the product manifold of positive numbers followed by a reprojection onto a subset of the probability simplex consisting of vectors whose components are bounded away from zero by a small constant. While such boundedness away from zero is necessary to avoid an arithmetic underflow, our convergence results imply that they are also necessary for theoretical reasons. Numerical examples show that the proposed simple and fast algorithm leads to very good results. In particular we apply the method for the partitioning of manifold-valued images. }, } - BergmannWeinmann-2016
Bergmann, R., Weinmann, A.2016A second order TV-type approach for inpainting and denoising higher dimensional combined cyclic and vector space data
Journal of Mathematical Imaging and Vision553401–427In this paper we consider denoising and inpainting problems for higher dimensional combined cyclic and linear space valued data. These kind of data appear when dealing with nonlinear color spaces such as HSV, and they can be obtained by changing the space domain of, e.g., an optical flow field to polar coordinates. For such nonlinear data spaces, we develop algorithms for the solution of the corresponding second order total variation (TV) type problems for denoising, inpainting as well as the combination of both. We provide a convergence analysis and we apply the algorithms to concrete problems.
@article{BergmannWeinmann-2016, number = {3}, pages = {401–427}, doi = {10.1007/s10851-015-0627-3}, author = {Bergmann, R. and Weinmann, A.}, eprint = {1501.02684}, year = {2016}, eprinttype = {arXiv}, volume = {55}, journaltitle = {Journal of Mathematical Imaging and Vision}, title = {A second order {TV}-type approach for inpainting and denoising higher dimensional combined cyclic and vector space data}, abstract = { In this paper we consider denoising and inpainting problems for higher dimensional combined cyclic and linear space valued data. These kind of data appear when dealing with nonlinear color spaces such as HSV, and they can be obtained by changing the space domain of, e.g., an optical flow field to polar coordinates. For such nonlinear data spaces, we develop algorithms for the solution of the corresponding second order total variation (TV) type problems for denoising, inpainting as well as the combination of both. We provide a convergence analysis and we apply the algorithms to concrete problems. }, } - BacakBergmannSteidlWeinmann-2016
Bačák, M., Bergmann, R., Steidl, G., Weinmann, A.2016A second order non-smooth variational model for restoring manifold-valued images
SIAM Journal on Scientific Computing381A567–A597We introduce a new non-smooth variational model for the restoration of manifold-valued data which includes second order differences in the regularization term. While such models were successfully applied for real-valued images, we introduce the second order difference and the corresponding variational models for manifold data, which up to now only existed for cyclic data. The approach requires a combination of techniques from numerical analysis, convex optimization and differential geometry. First, we establish a suitable definition of absolute second order differences for signals and images with values in a manifold. Employing this definition, we introduce a variational denoising model based on first and second order differences in the manifold setup. In order to minimize the corresponding functional, we develop an algorithm using an inexact cyclic proximal point algorithm. We propose an efficient strategy for the computation of the corresponding proximal mappings in symmetric spaces utilizing the machinery of Jacobi fields. For the -sphere and the manifold of symmetric positive definite matrices, we demonstrate the performance of our algorithm in practice. We prove the convergence of the proposed exact and inexact variant of the cyclic proximal point algorithm in Hadamard spaces. These results which are of interest on its own include, e.g., the manifold of symmetric positive definite matrices.
@article{BacakBergmannSteidlWeinmann-2016, number = {1}, pages = {A567–A597}, doi = {10.1137/15M101988X}, author = {Bačák, M. and Bergmann, R. and Steidl, G. and Weinmann, A.}, eprint = {1506.02409}, year = {2016}, eprinttype = {arXiv}, volume = {38}, journaltitle = {SIAM Journal on Scientific Computing}, title = {A second order non-smooth variational model for restoring manifold-valued images}, abstract = { We introduce a new non-smooth variational model for the restoration of manifold-valued data which includes second order differences in the regularization term. While such models were successfully applied for real-valued images, we introduce the second order difference and the corresponding variational models for manifold data, which up to now only existed for cyclic data. The approach requires a combination of techniques from numerical analysis, convex optimization and differential geometry. First, we establish a suitable definition of absolute second order differences for signals and images with values in a manifold. Employing this definition, we introduce a variational denoising model based on first and second order differences in the manifold setup. In order to minimize the corresponding functional, we develop an algorithm using an inexact cyclic proximal point algorithm. We propose an efficient strategy for the computation of the corresponding proximal mappings in symmetric spaces utilizing the machinery of Jacobi fields. For the $n$-sphere and the manifold of symmetric positive definite matrices, we demonstrate the performance of our algorithm in practice. We prove the convergence of the proposed exact and inexact variant of the cyclic proximal point algorithm in Hadamard spaces. These results which are of interest on its own include, e.g., the manifold of symmetric positive definite matrices. }, } - BergmannPerschSteidl-2016
Bergmann, R., Persch, J., Steidl, G.2016A parallel Douglas–Rachford algorithm for minimizing ROF-like functionals on images with values in symmetric Hadamard manifolds
SIAM Journal on Imaging Sciences93901–937We are interested in restoring images having values in a symmetric Hadamard manifold by minimizing a functional with a quadratic data term and a total variation like regularizing term. To solve the convex minimization problem, we extend the Douglas-Rachford algorithm and its parallel version to symmetric Hadamard manifolds. The core of the Douglas-Rachford algorithm are reflections of the functions involved in the functional to be minimized. In the Euclidean setting the reflections of convex lower semicontinuous functions are nonexpansive. As a consequence, convergence results for Krasnoselski-Mann iterations imply the convergence of the Douglas-Rachford algorithm. Unfortunately, this general results does not carry over to Hadamard manifolds, where proper convex lower semicontinuous functions can have expansive reflections. However, splitting our restoration functional in an appropriate way, we have only to deal with special functions namely, several distance-like functions and an indicator functions of a special convex sets. We prove that the reflections of certain distance-like functions on Hadamard manifolds are nonexpansive which is an interesting result on its own. Furthermore, the reflection of the involved indicator function is nonexpansive on Hadamard manifolds with constant curvature so that the Douglas-Rachford algorithm converges here.
Several numerical examples demonstrate the advantageous performance of the suggested algorithm compared to other existing methods as the cyclic proximal point algorithm or half-quadratic minimization. Numerical convergence is also observed in our experiments on the Hadamard manifold of symmetric positive definite matrices with the affine invariant metric which does not have a constant curvature.
@article{BergmannPerschSteidl-2016, number = {3}, pages = {901–937}, doi = {10.1137/15M1052858}, author = {Bergmann, R. and Persch, J. and Steidl, G.}, eprint = {1512.02814}, year = {2016}, eprinttype = {arXiv}, volume = {9}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {A parallel {D}ouglas–{R}achford algorithm for minimizing {ROF}-like functionals on images with values in symmetric {H}adamard manifolds}, abstract = { We are interested in restoring images having values in a symmetric Hadamard manifold by minimizing a functional with a quadratic data term and a total variation like regularizing term. To solve the convex minimization problem, we extend the Douglas-Rachford algorithm and its parallel version to symmetric Hadamard manifolds. The core of the Douglas-Rachford algorithm are reflections of the functions involved in the functional to be minimized. In the Euclidean setting the reflections of convex lower semicontinuous functions are nonexpansive. As a consequence, convergence results for Krasnoselski-Mann iterations imply the convergence of the Douglas-Rachford algorithm. Unfortunately, this general results does not carry over to Hadamard manifolds, where proper convex lower semicontinuous functions can have expansive reflections. However, splitting our restoration functional in an appropriate way, we have only to deal with special functions namely, several distance-like functions and an indicator functions of a special convex sets. We prove that the reflections of certain distance-like functions on Hadamard manifolds are nonexpansive which is an interesting result on its own. Furthermore, the reflection of the involved indicator function is nonexpansive on Hadamard manifolds with constant curvature so that the Douglas-Rachford algorithm converges here. Several numerical examples demonstrate the advantageous performance of the suggested algorithm compared to other existing methods as the cyclic proximal point algorithm or half-quadratic minimization. Numerical convergence is also observed in our experiments on the Hadamard manifold of symmetric positive definite matrices with the affine invariant metric which does not have a constant curvature. }, }
This work by Ronny Bergmann
is licensed under
CC BY-NC-SA 4.0.
Last modified: July 23, 2024.
Website built with Franklin.jl and the Julia programming language.