Die translationsinvarianten Räume sind seit Ende der 1980er Jahre ein wichtiges Werkzeug in der Zerlegung und Analyse von Daten und Funktionen. Sie stellen eine Funktion in verschiedenen Detailstufen dar, wobei sich auf jeder Stufe lokale Eigenschaften der Funktion in den Koeffizienten der Translate wiederfinden. Dazu ist es notwendig, dass die Funktionen einer solchen Zerlegung gut lokalisiert sind. Dies überträgt sich dann auf die von den Translaten der Wavelets aufgespannten orthogonalen Komplemente innerhalb der gestaffelten Räume. Neben diesen theoretischen Eigenschaften haben vor allem die schnellen Algorithmen der Wavelet-Transformation zur großen Verbreitung und Anwendung der Wavelets geführt. In den 1990er Jahren wurden periodische Wavelets entwickelt und in den letzten Jahren mehrdimensionale Wavelets, wie die Shearlets oder Curvelets, die insbesondere spezielle Richtungen in der Zerlegung einer Funktion bevorzugen.
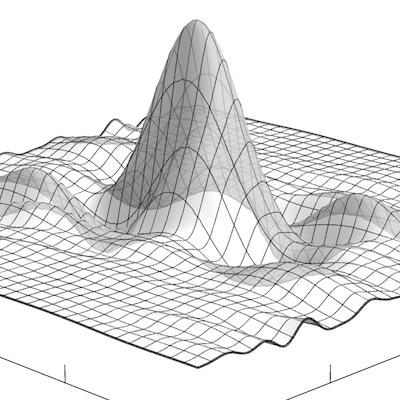
Diese Arbeit widmet sich den mehrdimensionalen periodischen translationsinvarianten Räumen, die insbesondere allgemeiner sind als diejenigen, die lediglich durch Tensorproduktbildung aus dem Eindimensionalen hervorgehen, und somit eine Anisotropie in ihren Fourier- Koeffizienten besitzen und gewisse Richtungseigenschaften haben. Diese Richtungspräferenz spiegelt sich auch in den Mustern wider, mit denen die Translate der Funktionen die hier betrachteten Räume bilden.
Zunächst wird für die periodischen translationsinvarianten Räume auf dem Torus der Interpolationsfehler betrachtet. Dazu werden die anisotropen periodischen Strang-Fix-Bedingungen eingeführt und mit ihnen Fehlerabschätzungen angegeben, welche die Räume bezüglich der Approximationsgüte für Funktionen mit bestimmten Glattheitseigenschaften charakterisieren.
Für die anisotrope periodische Wavelet-Transformation werden Algorithmen vorgestellt, die in ihrer Komplexität den schnellen Algorithmen der eindimensionalen Wavelets entsprechen und dabei insbesondere dimensionsunabhängig sind. Wichtigste Werkzeuge sind dazu die schnelle Fourier-Transformation und die den Wavelets zu Grunde liegenden Zwei-Skalen-Gleichungen der Multiskalen-Analyse. Außerdem wird durch diese Beschreibung eine Richtungsklassifikation der betrachteten Wavelets auf den Mustern möglich.
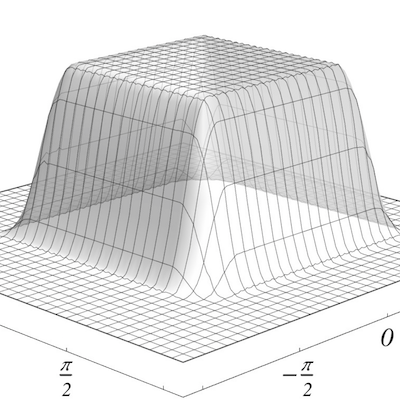
Ausgehend von den de la Vallée Poussin-Mitteln wird dann eine Verallgemeinerung vorgestellt, bei der lokalisierte anisotrope periodische Wavelets konstruiert werden, deren Fourier-Koeffizienten als Abtastung einer beliebig glatten Funktion gegeben sind, deren Träger endlich ist. Dies verallgemeinert sowohl die eindimensionalen de la Vallée Poussin-Wavelets als auch die multivariaten Dirichlet-Wavelets. Für spezielle glatte Funktionen gelingt es, in der Konstruktion anstelle der rekursiven Definition eine explizite Darstellung der Fourier-Koeffizienten anzugeben und somit für diese lokalisierten Wavelets eine gesamte Multiskalen-Analyse zu konstruieren.