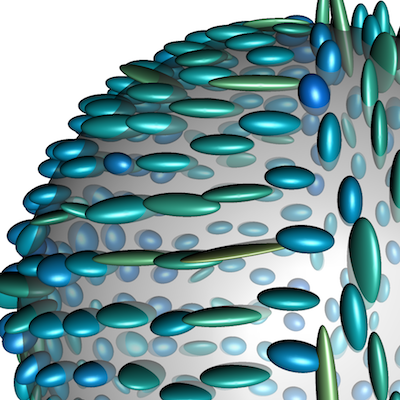
Graph-based methods have been proposed as a unified framework for discrete calculus of local and nonlocal image processing methods in the recent years. In order to translate variational models and partial differential equations to a graph, certain operators have been investigated and successfully applied to real-world applications involving graph models. So far the graph framework has been limited to real- and vector-valued functions on Euclidean domains. In this paper we generalize this model to the case of manifold-valued data. We introduce the basic calculus needed to formulate variational models and partial differential equations for manifold-valued functions and discuss the proposed graph framework for two particular families of operators, namely, the isotropic and anisotropic graph -Laplacian operators, . Based on the choice of we are in particular able to solve optimization problems on manifold-valued functions involving total variation () and Tikhonov () regularization. Finally, we present numerical results from processing both synthetic as well as real-world manifold-valued data, e.g., from diffusion tensor imaging (DTI) and light detection and ranging (LiDAR) data.
Processing Manifold-valued Data on Finite Weighted Graphs
This project aims to investigate methods to perform image processing and data analysis on manifold-valued data defined on a graph. This reaches from defining meaningful models and differential operators for data on Riemannian manifolds, to deriving numerical optimization schemes to solve the related problems, to the investigation of theoretical properties as convergence rates and upper bounds, to finally applying derived algorithms to real world applications, e.g., in medical imaging.
References
- BergmannTenbrinck-2018
Bergmann, R., Tenbrinck, T.2018A graph framework for manifold-valued data
SIAM Journal on Imaging Sciences111325–360@article{BergmannTenbrinck-2018, issue = {1}, pages = {325–360}, doi = {10.1137/17M1118567}, author = {Bergmann, R. and Tenbrinck, T.}, eprint = {1702.05293}, year = {2018}, eprinttype = {arXiv}, volume = {11}, journaltitle = {SIAM Journal on Imaging Sciences}, title = {A graph framework for manifold-valued data}, abstract = { Graph-based methods have been proposed as a unified framework for discrete calculus of local and nonlocal image processing methods in the recent years. In order to translate variational models and partial differential equations to a graph, certain operators have been investigated and successfully applied to real-world applications involving graph models. So far the graph framework has been limited to real- and vector-valued functions on Euclidean domains. In this paper we generalize this model to the case of manifold-valued data. We introduce the basic calculus needed to formulate variational models and partial differential equations for manifold-valued functions and discuss the proposed graph framework for two particular families of operators, namely, the isotropic and anisotropic graph $p$-Laplacian operators, $p\geq 1$. Based on the choice of $p$ we are in particular able to solve optimization problems on manifold-valued functions involving total variation ($p=1$) and Tikhonov ($p=2$) regularization. Finally, we present numerical results from processing both synthetic as well as real-world manifold-valued data, e.g., from diffusion tensor imaging (DTI) and light detection and ranging (LiDAR) data. }, } - BergmannTenbrinck-2017
Bergmann, R., Tenbrinck, T.2017Nonlocal inpainting of manifold-valued data on finite weighted graphs
in: Nielsen, F., Barbaresco, F.: Geometric Science of Information – 3rd Conference on Geometric Science of Information604–612, Springer International Publishing arXiv 1704.06424Recently, there has been a strong ambition to translate models and algorithms from traditional image processing to non-Euclidean domains, e.g., to manifold-valued data. While the task of denoising has been extensively studied in the last years, there was rarely an attempt to perform image inpainting on manifold-valued data. In this paper we present a nonlocal inpainting method for manifold-valued data given on a finite weighted graph. We introduce a new graph infinity-Laplace operator based on the idea of discrete minimizing Lipschitz extensions, which we use to formulate the inpainting problem as PDE on the graph. Furthermore, we derive an explicit numerical solving scheme, which we evaluate on two classes of synthetic manifold-valued images.
@inproceedings{BergmannTenbrinck-2017, publisher = {Springer International Publishing}, pages = {604–612}, doi = {10.1007/978-3-319-68445-1}, booktitle = {Geometric Science of Information – 3rd Conference on Geometric Science of Information}, author = {Bergmann, R. and Tenbrinck, T.}, editor = {Nielsen, F. and Barbaresco, F.}, eprint = {1704.06424}, year = {2017}, eprinttype = {arXiv}, title = {Nonlocal inpainting of manifold-valued data on finite weighted graphs}, abstract = { Recently, there has been a strong ambition to translate models and algorithms from traditional image processing to non-Euclidean domains, e.g., to manifold-valued data. While the task of denoising has been extensively studied in the last years, there was rarely an attempt to perform image inpainting on manifold-valued data. In this paper we present a nonlocal inpainting method for manifold-valued data given on a finite weighted graph. We introduce a new graph infinity-Laplace operator based on the idea of discrete minimizing Lipschitz extensions, which we use to formulate the inpainting problem as PDE on the graph. Furthermore, we derive an explicit numerical solving scheme, which we evaluate on two classes of synthetic manifold-valued images. }, }
This work by Ronny Bergmann
is licensed under
CC BY-NC-SA 4.0.
Last modified: February 18, 2026.
Website built with Franklin.jl and the Julia programming language.